Main

Three key predicted signatures of the elastic cotunnelling and crossed Andreev reflection (CAR) processes, shown schematically in Fig. 1, are (1) the coupling created between the normal probes is non-local—no current need be sent between them, (2) the resultant non-local signals decay rapidly as the probe separation is increased, exponentially over a superconducting coherence length ξS or faster4,5,7 and (3) the processes create quantum phase coherence between the two probes. Previous experiments looking for evidence of elastic cotunnelling and CAR have used normal–superconductor–normal and ferromagnet–superconductor–ferromagnet devices. A current is sent across one normal–superconductor or ferromagnet–superconductor interface and non-local voltages are measured on the other normal or ferromagnet probe located less than a coherence length from the interface10,11,12. Although the measured non-local signals exhibit behaviour consistent with predictions (1) and (2), the coherent nature of the non-local signals has not been demonstrated. To establish the presence of non-local coherence, we have attached a hybrid normal–superconducting loop known as an Andreev interferometer13,14,15 to one of the normal probes in a normal–superconductor–normal device. Modifying the phase of the electrons in the normal part of the Andreev interferometer by threading a magnetic flux through the loop leads to oscillations in the resistance of the loop with a period equal to the superconducting flux quantum Φ0=h/2e. Periodic oscillations can also be seen in the non-local resistance measured using normal probes placed off the interferometer, but coupled to it by a superconducting wire of length comparable to ξS. These oscillations are the result of CAR/elastic-cotunnelling processes that couple the non-local probes to flux-dependent quasiparticle currents in the normal arm of the Andreev interferometer.

Figure 1: CAR and elastic cotunnelling.
figure 1

If two normal metals attached to a superconductor are separated by less than the superconducting coherence length ξS, the wavefunction of the entangled Cooper pair of two electrons in the superconductor can interact with both normal metals simultaneously. In this geometry, two coherent processes are possible. a, CAR, wherein a Cooper pair is broken up into two phase-coherent electrons with one electron entering each of the spatially separated normal metals. b, Elastic cotunnelling, wherein an electron in one normal metal undergoes Cooper-pair-mediated tunnelling through the superconductor into the second normal metal. For the same configuration, these processes produce voltages of opposite signs, but both allow phase modulations of electrons in one normal metal to be coherently communicated to the other.

Full size image

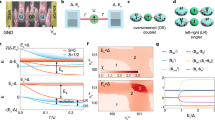
Figure 2a shows a scanning electron micrograph of a hybrid loop device. Although three devices with slightly different geometries were measured (see Supplementary Fig. S1), all show consistent results and here we concentrate on a single device with the geometry shown in Fig. 2a. At the centre of the device is a square loop ∼1.7 μm on each side formed from lines of 80 nm width. The loop is composed of 80-nm-thick Al lines on three sides and a 50-nm-thick Au wire on one side. Two superconducting leads attached to the loop on the left and two normal leads on the right serve as current and voltage probes for four-terminal measurements of the loop. Extra normal-metal voltage probes are placed on the right side of the loop at the top and bottom corners, and non-locally, just off the loop. The non-local probes are coupled to the normal part of the loop through a superconducting section of length 110 nm, comparable to the superconducting coherence length of Al in the dirty limit16.

Figure 2: Local interferometer measurements.
figure 2

a, Scanning electron micrograph of a hybrid normal-metal/superconducting loop with non-local normal leads 110 nm to the right of the loop. The scale bar is 1 μm. The bright wires are normal Au leads and the darker wires superconducting Al. The labelled current/voltage configuration is used to measure the local resistance of the loop. In addition to a small a.c. measurement current, a d.c. current can be applied to measure differential resistance at different d.c. biases. An external field can also be applied to thread a flux through the loop with the convention that a positive flux corresponds to a flux pointing into the page. The inset shows the resistance oscillations of the loop as function of flux, which have a Φ0=h/2e period. b, Local resistance of the hybrid loop as a function of temperature. The Al section of the loop undergoes a superconducting transition at 1.2 K; the remaining normal-arm resistance gradually decreases as the temperature is lowered owing to an increased superconducting proximity effect. At temperatures below 70 mK, the residual resistance starts to sharply decrease, although the normal section retains a finite resistance at the base temperature of our dilution refrigerator. Inset: The differential resistance of the loop at 14 mK as a function of current. The sharp decrease in the temperature-dependent resistance at low temperature is mirrored by a sharp change in the differential resistance for d.c. currents at ∼1 μA. Robust phase-coherent behaviour, such as shown in the inset of a, is observable only in this low-current, low-temperature regime.

Full size image

Figure 2b and the inset of Fig. 2a show data for the resistance of the loop using the current and voltage lead configuration marked in Fig. 2a. This is the local measurement configuration. As a function of temperature, the resistance undergoes a sharp drop at 1.2 K as the Al sections become superconducting, and the remaining resistance of the normal side gradually decreases as the loop is cooled further owing to the superconducting proximity effect. At 70 mK, the resistance begins to decline more sharply, although even at 14 mK, the base temperature of our refrigerator, the loop has a residual resistance above 1 Ω. The energy scale at which the superconducting proximity effect encompasses the normal section of the loop is given by the Thouless energy Ec=ℏD/L2, where L is the length of the normal section and D is the electron diffusion coefficient. Using measurements of a simultaneously fabricated Au wire to determine D=110 cm2 s−1 gives Ec=2.5 μeV for the L=1.7 μm normal side of the loop. This energy corresponds to a temperature of 30 mK, indicating that the low-temperature resistance drop of the loop is due to its transitioning into the correlation regime, where the time it takes electrons to traverse the normal-metal section is less than the decoherence time due to thermal energy. This regime can also be seen in the differential resistance measurements of the loop at 14 mK, where a sharp increase can be seen over a ±1 μA range. Robust coherent behaviour in the hybrid loop such as the large h/2e periodic resistance oscillations shown as an inset to Fig. 2a is observed in this correlation regime only below ±1 μA d.c. current and 70 mK.

As shown in Fig. 3a, to measure a phase-coherent non-local signal due to elastic cotunnelling and CAR, a phase-dependent quasiparticle current Iqp(Φ) needs to be injected from one normal probe into the superconductor while a non-local voltage is measured on a second probe VN relative to the superconductor potential VS. If an observed non-local voltage is due to a phase-coherent process, tuning the phase of Iqp(Φ) will reveal a phase-dependent non-local voltage. Iqp(Φ) is established by embedding the first probe in our interferometer (Fig. 3b) and adding a small d.c. current below 1 μA that is modulated by an a.c. measurement current. As discussed below, the small but finite d.c. current creates a non-equilibrium quasiparticle distribution in the normal arm of the loop that is necessary in these devices to establish Iqp(Φ) and the resulting phase-dependent non-local voltages. Similar to the local measurement above, the phase of Iqp(Φ) is tuned by an external flux through the interferometer loop. Although the current path of the local configuration marked in Fig. 2a may be used, any path along or intersecting the normal arm of the interferometer produces a non-equilibrium quasiparticle distribution in the arm, leading to similar qualitative effects. These effects are also independent of any non-equilibrium distribution induced in the non-local voltage probes (see Supplementary Fig. S2). We present results for the current path of Fig. 3b, where the current crosses only the centre of the loop, as it helps to emphasize the non-local nature of the measurement and illuminates the physics of the device.

Figure 3: Coherent non-local signals.
figure 3

a, Schemata of the configuration used to measure non-local Cooper-pair-mediated phase coherence. A phase-dependent quasiparticle current Iqp(Φ) is sent along a normal-metal probe into a superconductor. The elastic cotunnelling and CAR processes couple the voltages created by this current into a second normal probe VN located ∼ξS from the first, although no current is sent between the two normal probes. The voltage VN is measured relative to the superconducting condensate potential VS as the phase of Iqp(Φ) is varied. b, To create Iqp(Φ), the first probe is embedded in an Andreev interferometer through which a 250 nA d.c. current is driven to create a non-equilibrium quasiparticle distribution in the normal section of the loop. The resultant differential voltages, normalized by a low-frequency (<100 Hz) a.c. measurement current added to the d.c. current, are measured on both the corner probes on the loop (subscript C) and non-local probes off the loop (subscript N). These voltages are modulated by an external flux through the loop that can tune Iqp(Φ). Taken at 14 mK, the oscillating signals seen on the probes at the corners of the loop are picked up on the non-local probes through elastic cotunnelling and CAR. The signals are greatly attenuated on the non-local probes, consistent with the expected distance dependence of these coherent processes. For a given flux, the voltages on the leads at the top and bottom of the loop (superscripts T and B) have opposite polarities.

Full size image

Using this current configuration, we measure the differential voltage signals (normalized by the a.c. measurement current amplitude) on the non-local probes off the loop (subscript N) as well as the leads on the corner of the loop (subscript C) relative to the superconductor potential VS. We also compare the signals seen at the top and bottom of the loop (superscripts T and B). Figure 3 exhibits the flux-dependent voltages on these four probes. The signals on the non-local probes, VNT and VNB, show oscillations with the Φ0 flux period dictated by the geometry of the loop. Thus, the quasiparticles in the non-local probes off the loop are being coupled to the phase-coherent processes on the loop, consistent with the predicted elastic cotunnelling and CAR effects. In addition to the coherent nature of these non-local signals, the decay of this signal along the superconductor confirms that they are due to elastic cotunnelling and CAR. The oscillations on the VCT and VCB corner leads are identical in behaviour to the oscillations on their respective non-local leads, but with an amplitude six times as large. The strong attenuation of the signals along the 110 nm from the corner to non-local leads is consistent with an expected dependence on the superconducting coherence length ξS for elastic cotunnelling and CAR processes4,5,7.

As we noted above, the non-local signals shown in Fig. 3 arise from a phase-dependent quasiparticle current Iqp(Φ) in the normal arm of the loop. The origin of Iqp(Φ) can be understood by examining in detail the effect of the non-equilibrium quasiparticle distribution induced by the d.c. current. Within the framework of the quasiclassical theory of superconductivity (see the Methods section), the current between the two normal–superconductor interfaces can be expressed as17

Here, N0 is the quasiparticle density of states at the Fermi energy, T is the temperature, M33 and M03 are normalized diffusion coefficients that depend on the energy E and spatial coordinates R and Q is the energy-dependent spectral supercurrent. hT and hL are space-dependent quasiparticle distribution functions that have the equilibrium values

at a reservoir (either superconducting or normal) with an applied voltage V. In particular, at the superconducting reservoirs at the normal–superconductor interface, where we assume V is 0 with no loss of generality, hT=0 and hL=tanh(E/2kBT).

At low temperatures, where the quasiparticle inelastic scattering length is very long, application of a d.c. current as shown in Fig. 3b will result in non-equilibrium space-dependent distribution functions hT and hL in the normal arm of the interferometer. As has already been demonstrated experimentally in superconductor–normal–superconductor junctions, this can affect the total supercurrent through the second term in the brackets in equation (1), even leading to reversal in sign of the critical current, the so-called tunable π-junction18,19,20. In our sample, the application of the d.c. current results in the value of hL at the midpoint of the normal arm of the Andreev interferometer being different from its value at either normal–superconductor interface. As the spectral supercurrent Q is conserved, the total supercurrent, given by the integral of Q hL over the energy E also varies as a function of position along the normal arm. The conservation of the total current then implies that there is a compensating quasiparticle current arising from the first and third terms in the brackets in equation (1) (ref. 21).

Simulations based on the quasiclassical theory (see the Methods section) show that hL varies appreciably only in the vicinity of the normal–superconductor interfaces, so that these quasiparticle currents are also appreciable only in the vicinity of the normal–superconductor interfaces. As the supercurrent is periodic in the applied flux, the induced Iqp is also periodic in the applied flux, giving rise to a periodic non-local resistance through CAR/elastic-cotunnelling processes7. Figure 4b shows Iqp arising from the first term in the brackets in equation (1) near the normal–superconductor interface as a function of the phase difference Δφ between the two normal–superconductor interfaces at a finite voltage V =3Ec applied between the normal reservoirs. The calculated Iqp is periodic and antisymmetric in Δφ. Whereas the calculated circulating currents are approximately sinusoidal in Δφ, the measured non-local voltages have a slightly more sawtooth dependence on the applied flux; this is due to self-flux effects associated with the finite inductance of the Andreev interferometer22,23,24. Furthermore, the fact that the signals measured at the top and bottom corners are of opposite sign is consistent with the fact that Iqp goes from the superconductor to the normal arm of the Andreev interferometer at one normal–superconductor interface, whereas it goes from the normal arm into the superconductor at the second normal–superconductor interface.

Figure 4: Comparison with quasiclassical simulations.
figure 4

a, Single differential voltage oscillation on the VCB probe in Fig. 3 as a function of flux through the interferometer. b, Supercurrent and quasiparticle current in the normal arm as a function of the phase difference Δφ between the two superconducting interfaces, calculated by solving the quasiclassical equations of superconductivity for diffusive systems for the model system shown in the inset. The geometry is a normal-metal cross connected to two superconducting reservoirs and two normal reservoirs, with a voltage difference V applied between the normal reservoirs. The calculation in this figure is for eV=3Ec. c, Differential resistance measured on the VCT probe as a function of the applied d.c. current with a flux of Φ0/4 threading the Andreev interferometer. d, Supercurrent (red curve) calculated at the midpoint of the normal arm of the interferometer, and differential resistance (black curve) as a function of applied voltage, at a phase difference of Δφ=π/2, corresponding to a flux of Φ0/4 through the loop.

Full size image

Figure 4c shows VCT as a function of the injected d.c. current with an applied flux of Φ0/4 through the interferometer, approximately the flux at which the maximum signal is observed. The signal oscillates as a function of the d.c. current, vanishing at zero d.c. current and high d.c. currents. This dependence on the d.c. current is strongly reminiscent of the behaviour of the supercurrent in multi-terminal normal–superconductor devices that has been predicted and observed experimentally18,19,20. Figure 4d shows the calculated differential resistance as a function of the voltage V (proportional to the applied d.c. current), which reproduces qualitatively the behaviour we see in our experiments. Our experiments show, and the simulations predict, that the quasiparticle current Iqp is present only when there is a non-equilibrium distribution in the normal arm of the loop. It is only under non-equilibrium conditions that a conversion of supercurrent to quasiparticle current can occur.

Methods

Experimental.

Our devices are fabricated using photo and electron-beam lithography on Si substrates with 300 nm SiO2 insulating layers. The critical features are patterned in spun methyl methacrylate/polymethyl methacrylate bilayers using a Tescan MIRA electron microscope. The 99.999% pure Au and Al films are deposited in an Edwards thermal evaporator with a base pressure of 3×10−7 torr. Before the Au deposition, in situ O2+ plasma etching is carried out to clean the substrate, and before the Al deposition in situ Ar+ plasma etching is carried out to ensure clean interfaces between the two materials. After the Al deposition, the devices are loaded into an Oxford dilution refrigerator and cooled to 77 K within a few hours to prevent degradation of the interfaces. Measurements of our interfaces show a barrier resistivity of 1.9 μm2 Ω, comparable to the Sharvin resistivity.

Measurements were carried out using PAR 124 lock-in amplifiers with modified Adler–Jackson resistance bridges25. The bridges can introduce small, ≲100 mΩ, offsets to the data, which are removed by cross-checking the measured resistance using a true four-terminal measurement with a current source and lock-in amplifier. Low-frequency (<100 Hz) a.c. measurement currents at two different frequencies and amplitudes of 20 and 100 nA were used for local and non-local measurements respectively, with 5 nA currents used to check against the possibility of effects due to heating. To remove extraneous noise signals, first-stage amplification of the measurement signals occurred in a mu-metal-shielded enclosure attached to the cryostat.

Theoretical

The simulations were done by solving the Usadel equations of quasiclassical superconductivity in the so-called θ parametrization for the geometry shown in the inset to Fig. 4b. Using the formalism of ref. 17, these equations can be written in the normal wires as

and

Here, χ is the complex gauge-invariant phase, and

where the spectral supercurrent Q is related to js by . In the normal wire, ∂RQ=0. In addition, we have the condition that the spectral electronic current j(E,R)=M33∂RhT+Q hL+M03∂RhL and the spectral thermal current jth(E,R)=M00∂RhL+Q hT+M30∂RhT are conserved, that is, ∂Rj(E,R)=0 and ∂Rjth(E,R)=0. Here, the normalized diffusion coefficients M are given by , and M30=−M03.

The solutions to these coupled equations are obtained by first solving equations (3) and (4) for the complex θ and χ for the geometry of the inset to Fig. 4b along all four normal wires of the cross, using a numerical relaxation technique and appropriate boundary conditions. The boundary conditions at a normal reservoir are that θ and χ vanish. The phase difference Δφ is dropped symmetrically between the superconducting reservoirs, being set to Δφ/2 at one superconducting reservoir, and −Δφ/2 at the other, as shown in the inset to Fig. 4b. The boundary condition for θ at a superconducting reservoir is given by θS0=−i(π/2)+(1/2)ln[(|Δ|+E)/(|Δ|−E)], if E<|Δ|, and θS0=(1/2)ln[(E+|Δ|)/(E−|Δ|)], if E>|Δ|, where Δ is the gap in the superconducting reservoir. The boundary conditions at the node where all four wires meet are that θ and χ are continuous, and that the sum of their derivatives is equal to 0.

After θ and χ are obtained, the kinetic equations ∂Rj(E,R)=0 and ∂Rjth(E,R)=0 are then solved using a numerical relaxation technique, subject to the boundary conditions on hT and hL at the reservoirs given by equation (2). We assume the voltage applied to the normal reservoirs is dropped symmetrically between them, as shown in the inset to Fig. 4b. The quasiparticle current shown in Fig. 4b is given by the integral of M33∂RhT over the energy E, that is, the first term in the brackets in equation (1); the supercurrent is given by the second term. (The contribution of the third term is much smaller than that of the first term, but has a similar qualitative dependence.) To calculate the differential resistance dV/dI shown in Fig. 4d, we take the derivative of Iqp calculated as above with respect to V. As the voltage V is linearly related to the d.c. current by the resistance of the normal wires connected to the normal reservoirs, and the non-local voltage measured should also be linearly related to the quasiparticle current in the non-local normal arm through elastic-cotunnelling/CAR, this quantity is the same as dV/dI to within a numerical factor.