Abstract
The experimental progress achieved in parity–time ( ) symmetry in classical optics1,2,3,4,5,6,7,8,9,10,11,12,13,14 is the most important accomplishment in the past decade15 and stimulates many new applications, such as unidirectional light transport5,6,7,8 and single-mode lasers12,13. However, in the quantum regime, some controversial effects are proposed for
) symmetry in classical optics1,2,3,4,5,6,7,8,9,10,11,12,13,14 is the most important accomplishment in the past decade15 and stimulates many new applications, such as unidirectional light transport5,6,7,8 and single-mode lasers12,13. However, in the quantum regime, some controversial effects are proposed for  -symmetric theory16,17,18,19, for example, the potential violation of the no-signalling principle19. It is therefore important to understand whether
-symmetric theory16,17,18,19, for example, the potential violation of the no-signalling principle19. It is therefore important to understand whether  -symmetric theory is consistent with well-established principles. Here, we experimentally study this no-signalling problem related to the
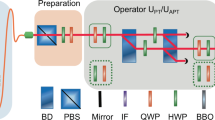
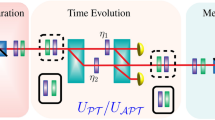
-symmetric theory is consistent with well-established principles. Here, we experimentally study this no-signalling problem related to the  -symmetric theory using two space-like separated entangled photons, with one of them passing through a post-selected quantum gate, which effectively simulates a
-symmetric theory using two space-like separated entangled photons, with one of them passing through a post-selected quantum gate, which effectively simulates a  -symmetric evolution. Our results suggest that the superluminal information transmission can be simulated when the successfully
-symmetric evolution. Our results suggest that the superluminal information transmission can be simulated when the successfully  -symmetrically evolved subspace is solely considered. However, considering this subspace is only a part of the full Hermitian system, additional information regarding whether the
-symmetrically evolved subspace is solely considered. However, considering this subspace is only a part of the full Hermitian system, additional information regarding whether the  -symmetric evolution is successful is necessary, which transmits to the receiver at maximally light speed, maintaining the no-signalling principle.
-symmetric evolution is successful is necessary, which transmits to the receiver at maximally light speed, maintaining the no-signalling principle.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout


 gate.
gate.

Similar content being viewed by others
References
Ruschhaupt, A., Delgado, F. & Muga, J. G. Physical realization of -symmetric potential scattering in a planar slab waveguide. J. Phys. A 38, L171–L176 (2005).
Klaiman, S., Günther, U. & Moiseyev, N. Visualization of branch points in -symmetric waveguides. Phys. Rev. Lett. 101, 080402 (2008).
Guo, A. et al. Observation of -symmetry breaking in complex optical potentials. Phys. Rev. Lett. 103, 093902 (2009).
Rüter, C. E. et al. Observation of parity–time symmetry in optics. Nature Phys. 6, 192–195 (2010).
Feng, L. et al. Experimental demonstration of a unidirectional reflectionless parity-time metamaterial at optical frequencies. Nature Mater. 12, 108–113 (2013).
Feng, L. et al. Nonreciprocal light propagation in a silicon photonic circuit. Science 333, 729–733 (2011).
Peng, B. et al. Parity–time-symmetric whispering-gallery microcavities. Nature Phys. 10, 394–398 (2014).
Chang, L. et al. Parity–time symmetry and variable optical isolation in active-passive-coupled microresonators. Nature Photon. 8, 524–529 (2014).
Chong, Y. D., Ge, L. & Stone, A. D. -symmetry breaking and laser-absorber modes in optical scattering systems. Phys. Rev. Lett. 106, 093902 (2011).
Liertzer, M. et al. Pump-induced exceptional points in lasers. Phys. Rev. Lett. 108, 173901 (2012).
Brandstetter, M. et al. Reversing the pump dependence of a laser at an exceptional point. Nature Commun. 5, 4034 (2014).
Feng, L., Wong, Z. J., Ma, R.-M., Wang, Y. & Zhang, X. Single-mode laser by parity-time symmetry breaking. Science 346, 972–975 (2014).
Hodaei, H., Miri, M.-A., Heinrich, M., Christodoulides, D. N. & Khajavikhan, M. Parity-time-symmetric microring lasers. Science 346, 975–978 (2014).
Regensburger, A. et al. Parity–time synthetic photonic lattices. Nature 488, 167–171 (2012).
Cham, J. Top 10 physics discoveries of the last 10 years. Nature Phys. 11, 799 (2015).
Croke, S. -symmetric Hamiltonians and their application in quantum information. Phys. Rev. A 91, 052113 (2015).
Bender, C. M., Brody, D. C., Jones, H. F. & Meister, B. K. Faster than Hermitian quantum mechanics. Phys. Rev. Lett. 98, 040403 (2007).
Bender, C. M. et al. -symmetric quantum state discrimination. Phil. Trans. R. Soc. A 371, 20120160 (2013).
Lee, Y.-C., Hsieh, M.-H., Flammia, S. T. & Lee, R.-K. Local symmetry violates the no-signaling principle. Phys. Rev. Lett. 112, 130404 (2014).
Shankar, R. Principles of Quantum Mechanics (Springer, 1994).
Bender, C. M. & Boettcher, S. Real spectra in non-Hermitian Hamiltonians having symmetry. Phys. Rev. Lett. 80, 5243–5246 (1998).
Bender, C. M., Boettcher, S. & Meisinger, P. N. -symmetric quantum mechanics. J. Math. Phys. 40, 2201–2229 (1999).
Bender, C. M., Brody, D. C. & Jones, H. F. Complex extension of quantum mechanics. Phys. Rev. Lett. 89, 270401 (2002).
Günther, U. & Samsonov, B. F. Naimark-dilated -symmetric brachistochrone. Phys. Rev. Lett. 101, 230404 (2008).
Günther, U. & Samsonov, B. F. -symmetric brachistochrone problem, Lorentz boosts, and nonunitary operator equivalence classes. Phys. Rev. A 78, 042115 (2008).
Mostafazadeh, A. Pseudo-Hermiticity versus symmetry: The necessary condition for the reality of the spectrum of a non-Hermitian Hamiltonian. J. Math. Phys. 43, 205–214 (2002).
Brody, D. C. Consistency of -symmetric quantum mechanics. J. Phys. A 49, 10LT03 (2016).
Schindler, J., Li, A., Zheng, M. C., Ellis, F. M. & Kottos, T. Experimental study of active LRC circuits with symmetries. Phys. Rev. A 84, 040101(R) (2011).
Ramezani, H., Schindler, J., Ellis, F. M., Günther, U. & Kottos, T. Bypassing the bandwidth theorem with symmetry. Phys. Rev. A 85, 062122 (2012).
Hensen, B. et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 526, 682–686 (2015).
Giustina, M. et al. Significant-loophole-free test of Bell's theorem with entangled photons. Phys. Rev. Lett. 115, 250401 (2015).
Shalm, L. K. et al. Strong loophole-free test of local realism. Phys. Rev. Lett. 115, 250402 (2015).
L'Ecuyer, P. & Simard, R. TestU01: A C library for empirical testing of random number generators. ACM Trans. Math. Softw. 33, 22 (2007).
Acknowledgements
We are grateful to C. J. Zhang, Y. C. Lee and D. C. Brody for valuable discussions. This work is supported by the National Natural Science Foundation of China (Grants numbers 61490711, 11474267, 11274289, 11304305, 11325419, 61327901 and 91321313), the Strategic Priority Research Program(B) of the Chinese Academy of Sciences (Grant No. XDB01030300). C-F.L. acknowledges support from the EU Collaborative project QuProCS (641277).
Author information
Authors and Affiliations
Contributions
C-F.L., J-S.T., Y-T.W. and Y-J.H. planned and designed the experiments. J-S.T., Y-T.W. and S.Y. implemented the experiments with the help of J-S.X. and B-H.L. D-Y.H. fabricated the home-made circuit. C-F.L., Y-J.H., J-S.T., Y-T.W., G.C., Y-N.S. and K.S. carried out the theoretical analysis and developed the interpretation. J-S.T. and Y-J.H. wrote the paper with the help of C-F.L. and Y-T.W., and all authors discussed its contents. Y-J.H. supervised the theoretical part of the project. G-C.G. and C-F.L. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 332 kb)
Rights and permissions
About this article
Cite this article
Tang, JS., Wang, YT., Yu, S. et al. Experimental investigation of the no-signalling principle in parity–time symmetric theory using an open quantum system. Nature Photon 10, 642–646 (2016). https://doi.org/10.1038/nphoton.2016.144
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphoton.2016.144
This article is cited by
-
Demonstration of \(\mathcal{P}\mathcal{T}\)-symmetric quantum state discrimination
Quantum Information Processing (2024)
-
Extension of Noether’s theorem in \({\cal P}{\cal T}\)-symmetry systems and its experimental demonstration in an optical setup
Science China Physics, Mechanics & Astronomy (2023)
-
Experimental demonstration of the dynamics of quantum coherence evolving under a PT-symmetric Hamiltonian on an NMR quantum processor
Quantum Information Processing (2022)
-
Uncertainty of quantum channels via modified generalized variance and modified generalized Wigner–Yanase–Dyson skew information
Quantum Information Processing (2022)
-
Searching for exceptional points and inspecting non-contractivity of trace distance in (anti-)\(\mathcal {PT}\!\)-symmetric systems
Quantum Information Processing (2022)