Abstract
Extreme optical properties can be realized by the strong resonant response of metamaterials consisting of subwavelength-scale metallic resonators. However, highly dispersive optical properties resulting from strong resonances have impeded the broadband operation required for frequency-independent optical components or devices. Here we demonstrate that strong, flat broadband optical activity with high transparency can be obtained with meshed helical metamaterials in which metallic helical structures are networked and arranged to have fourfold rotational symmetry around the propagation axis. This nondispersive optical activity originates from the Drude-like response as well as the fourfold rotational symmetry of the meshed helical metamaterials. The theoretical concept is validated in a microwave experiment in which flat broadband optical activity with a designed magnitude of 45° per layer of metamaterial is measured. The broadband capabilities of chiral metamaterials may provide opportunities in the design of various broadband optical systems and applications.
Similar content being viewed by others
Introduction
Polarization is one of the most fundamental and important aspects of electromagnetic waves. The manipulation of the polarization state is crucial in the design and realization of various optical systems because the electromagnetic response of a material or a device generally depends on the polarization states of incident electromagnetic waves. Traditionally, manipulation of polarization states has been achieved by the use of wave plates, gratings1, prismatic rotators2 or natural chiral media3. Compared with other devices, chiral media have an intrinsic benefit of requiring no rotational adjustment; the rotational state of the chiral media around their own optical axis does not affect the optical rotatory power. The term ‘chiral’ refers to the structural characteristic of an object that lacks any mirror symmetries. In chiral media, electric and magnetic fields are cross-coupled, so that the degeneracy between right and left circularly polarized waves (RCP and LCP waves) is lifted. This broken degeneracy results in nonidentical refractive indices for the RCP and LCP waves. As a result, the polarization plane of a linearly polarized, electromagnetic wave travelling in chiral media is rotated, and this phenomenon is called optical activity. However, the strength of optical activity in natural chiral media is small and dispersive, thus rendering broadband polarization rotation inefficient with natural chiral media.
In recent years, chiral media that possess strong chirality have been constructed artificially. Much attention has been focused on their potential route to negative refraction/reflection4,5,6,7,8,9,10,11,12, asymmetric transmission13,14,15,16,17 and the observation of repulsive Casimir force18,19, as well as their gigantic optical activity and circular dichroism8,9,12,20,21,22,23,24,25,26,27,28,29,30. Utilizing strongly resonant, chiral meta-molecules, the limitation of weak optical activity can be overcome. Yet, despite unnaturally strong chirality of resonant-type chiral metamaterials, highly dispersive optical activity and corresponding narrow transmission bandwidth still were hampering the achievement of broadband polarization manipulation7,9,12,20,21,26. Recently, there have been a few attempts to achieve nondispersive optical activity with metamaterials based on complementary configurations; however, the intrinsic resonant properties of the meta-atoms that were used still limited the operating bandwidth31,32. Furthermore, two characteristic optical properties of chiral media, that is, circular birefringence and dichroism, coexist in the operating frequency band so that the realization of pure broadband optical activity is a critical and current issue for chiral metamaterials. In the presence of significant circular dichroism, a linearly polarized wave travelling through chiral metamaterials becomes elliptically polarized, which exemplifies the inadequacy of resonant chiral metamaterials as polarization rotators.
Here we demonstrate that extremely broadband, nondispersive, strong optical activity with high transparency can be obtained with nonresonant, meshed helical metamaterials (MHMs). This nonresonant behaviour of MHMs comes from their Drude-like response that results in 1/ω dispersion of effective chirality parameter κ. Furthermore, it is shown that circular dichroism is essentially absent in a wide range of operating frequencies. In contrast to other work based on an array of helices with parallel configuration24,33,34,35,36,37,38 or metallic gyroid structures with mixtures of right- and left-handed helices39,40, the double-helix structures in MHMs are networked and arranged with fourfold rotational symmetry around the wave propagation axis. To prove the nondispersive, strong optical activity of MHMs, samples designed to rotate the polarization state by 45° per layer are fabricated and measured. The optical rotary power of a single-layer MHM can be engineered by varying the thickness of the MHM wires, and the optical activity of the stacked MHMs can be made proportional to the number of layers. It also is found that the transmission bandwidth can be easily tailored by varying the interlayer spacing.
Results
Unit cell of MHMs
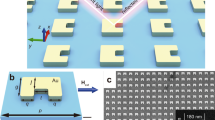
An MHM can be configured with double helical metallic structures as its building blocks (Fig. 1a). Within the MHM, the helices are arranged densely with fourfold rotational symmetry along the wave propagation axis. The rotational symmetry of metallic helical structures in MHMs leads to the nondispersive optical activity and extinction of circular dichroism. Furthermore, by utilizing the double helix as a building block rather than a single helix, the magnitude of optical activity can be enhanced in MHMs, similar to the case of parallel configuration of helical structures, where the circular dichroism is enhanced with double helix arrays41,42,43. The rotational symmetry of the unit cell assures the eigenpolarizations for MHMs under normal incidence to be a pair of circular polarizations44, which results in invariant optical properties for arbitrary input polarization angles. With the excitation of electromagnetic waves on MHMs, magnetic and electric dipole moments are induced in the transverse direction of the axis of wave propagation (Fig. 1a). These dipole moments can be excited by either an electric filed or a magnetic field parallel to the helical axis of each helix in the MHM. Figure 1b shows the magnetic field distribution in the plane of z=−h/2 when the incident electric field is polarized in the x direction, which clearly shows that the magnetic dipole moment is induced strongly along the parallel direction to the electric field of the incident wave. This strong magnetoelectric coupling leads to the large optical activity of MHMs. Figure 1c shows a photographic image of an MHM fabricated with acrylic resin and silver by commercial, layered-prototyping equipment. Utilizing a pair of linearly polarized, broadband horn antennas, the chiral properties of MHMs are characterized in microwave frequencies (see Methods).
(a) Schematic illustration of MHM. The unit cell is composed of four double-helix metallic structures (left side of the figure), densely arranged with fourfold rotational symmetry around the z axis that assures the incident polarization-independent property. The incident electric field E induces the surface current and electric dipole moment P. The current excites the strong magnetic dipole moment M along the parallel direction of P. (b) The numerically calculated H field distribution at z=−h/2 plane of unit cell (at 7.2 GHz) is shown with impinging electric field polarized in the direction of the x axis. (c) Photograph of the fabricated sample of MHM. The size of the fabricated sample was 170 × 170 mm. The lattice constant of the primitive unit cell (indicated as a red dashed square) is represented as α=3.66 mm. Samples with the following structural dimensions were tested: a=2.59 mm, w1=1.15 mm, w2=2.0 mm, t=0.50 mm and h=2.5 mm.
Nondispersive optical activity
The simulated and measured total transmission amplitudes, defined as  for a single-layer MHM, are plotted in Fig. 2a. The total transmission approaches nearly unity at 7.2 GHz, corresponding to the impedance-matching frequency to free space (Supplementary Fig. 1). Figure 2b shows the retrieved chirality parameter from the measurement and that calculated from a finite-difference time-domain (FDTD) simulation. It can be seen clearly that the real part of chirality parameter κ is proportional to 1/ω. The real part and the imaginary part of κ are related to the magnitude of circular birefringence and dichroism, respectively. The inverse proportionality of the real part of the chirality parameter to the frequency leads to the broadband and nondispersive optical activity (Fig. 2c), since the polarization rotation θ can be explicitly expressed as θ=Re(κ)·ωh/c0. From numerical calculations, the upper bound in the frequency range of the nearly nondispersive optical activity reaches ~42 GHz, at which a higher mode starts to dominate (Supplementary Fig. 2). Moreover, the ellipticity η is nearly zero over all measured frequency ranges, and, therefore, the polarization state of the transmitted wave still remains linearly polarized (Fig. 2d). It can be seen that all experimental results and simulations are in very good agreement.
for a single-layer MHM, are plotted in Fig. 2a. The total transmission approaches nearly unity at 7.2 GHz, corresponding to the impedance-matching frequency to free space (Supplementary Fig. 1). Figure 2b shows the retrieved chirality parameter from the measurement and that calculated from a finite-difference time-domain (FDTD) simulation. It can be seen clearly that the real part of chirality parameter κ is proportional to 1/ω. The real part and the imaginary part of κ are related to the magnitude of circular birefringence and dichroism, respectively. The inverse proportionality of the real part of the chirality parameter to the frequency leads to the broadband and nondispersive optical activity (Fig. 2c), since the polarization rotation θ can be explicitly expressed as θ=Re(κ)·ωh/c0. From numerical calculations, the upper bound in the frequency range of the nearly nondispersive optical activity reaches ~42 GHz, at which a higher mode starts to dominate (Supplementary Fig. 2). Moreover, the ellipticity η is nearly zero over all measured frequency ranges, and, therefore, the polarization state of the transmitted wave still remains linearly polarized (Fig. 2d). It can be seen that all experimental results and simulations are in very good agreement.
Drude-like response of MHMs
The nondispersive behaviour of optical activity can be attributed to the Drude-like response of MHMs. In general, resonant-type chiral metamaterials, for which the current distribution is localized in the unit cell, have distinct Lorentz-like electric and magnetic resonances, and the dispersive optical activity becomes inevitable near these resonance frequencies9,19,21,26,27,45. However, in the unit cell of the proposed MHM, four double-helix structures were interconnected so that the current flows freely through the metallic helix network with Drude-like behaviour. For an intuitive understanding of the nonresonant behaviour of MHMs, we developed an effective circuit model in which the double-helix structure in Fig. 1a (constituting a quadrant of the unit cell) was assumed to have total lumped inductance L and resistance R. Under electromagnetic excitation, the average electric displacement and magnetic flux density for a single-layer MHM can be derived as follows (see Methods):

where S is the cross-sectional area of a double helix, V0 is the volume of a unit cell and γ is the dissipation constant, defined as R/L. In correspondence with the constitutive equation of general chiral media with reciprocity, the effective chirality parameter of MHM can be estimated as:

Assuming negligible dissipation with a substrate-free metallic network at microwave frequencies, the chirality parameter assumes a real value, which results in an inverse proportionality between the chirality parameter and the frequency. This scaling law of the chirality parameter can be confirmed by numerical simulation and measurement (Fig. 2b–d). It is worthwhile noting that the imaginary part of κ in the transmission band is very small, even in the presence of significant dissipation because it decays very rapidly with ω−2 so that the real part of κ is dominant in the transmission band. Therefore, little circular dichroism exists for the transmitted waves, and, thus, linearly polarized input waves maintain their polarization states in MHMs.
Scaling of optical activity with a geometrical parameter
For proof of the concept with an experimental demonstration, the geometrical parameters of the MHMs were chosen specifically such that the polarization rotation was 45° for a single-layer MHM. However, optical rotary power can be tuned easily by varying the thickness t of the wire of the structure (Fig. 1a). Figure 3a shows the simulated polarization rotation for a single-layer MHM with variation in t, where the optical activity was found to be correlated strongly with the thickness of the wire. As can be seen in the plot, the optical activity becomes stronger with increasing t, while the nondispersive property still is preserved. In order to clearly show this scaling behaviour, the optical activity at 10 GHz was plotted in Fig. 3b as a function of t. This behaviour can be predicted by the analytical model with the lumped inductance L of a double helix approximated by  (refs 33, 46). Here K1 and K2 are structural fitting parameters that are dependent on the shapes of the inductors, t is the thickness of the wire and w is the effective mean diameter of the helices given by
(refs 33, 46). Here K1 and K2 are structural fitting parameters that are dependent on the shapes of the inductors, t is the thickness of the wire and w is the effective mean diameter of the helices given by  , which was introduced to simplify the equation (Fig. 1a). Substituting this inductance formula into equation (2), the expression for the polarization rotation after travelling a single-layer MHM can be written as:
, which was introduced to simplify the equation (Fig. 1a). Substituting this inductance formula into equation (2), the expression for the polarization rotation after travelling a single-layer MHM can be written as:
(a) Numerically calculated polarization rotation angle through a single-layer MHM depending on the thickness of the wire t of the helical structures with iso-angle lines (black dashed lines). The rotation angle is increased with the thickness of the wire, while the nondispersive property of optical activity was barely affected. (b) Simulated polarization rotation with varying t plotted at 10 GHz and fitted with the analytical model; the following fitting parameters were used: K1=0.331 and K2=3.384.

This scaling behaviour is plotted in Fig. 3b, and it fits well with the numerical simulation.
Tailoring the transmission bandwidth of MHMs
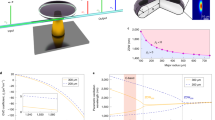
In general, the effective parameters of bulk metamaterials are different from those of a constituting metamaterial layer in the presence of strong interlayer coupling7,9,21,23,27,45,47,48. However, interlayer coupling between MHMs is negligibly small because the magnetic field in MHMs is highly localized inside the helices, as can be seen in Fig. 1b. Therefore, a single-layer MHM can be considered as a homogeneous thin film, and the transmission coefficients for stratified MHMs can be calculated by the characteristic matrix formalism49,50. With a numerically obtained matrix for a single-layer MHM, the transmission through double-layered MHMs with different interlayer spacing distances can be calculated as shown in Fig. 4a. The results from FDTD simulations also are plotted along with those from the characteristic matrix method in Fig. 4a and compared with the experimental data. In the measurements, we inserted polyethylene plates with three thicknesses, that is, s=1.5, 3.0 and 5.0 mm to certify the exact distance between the two layers. The agreement between the characteristic matrix method, FDTD simulation and experimental data confirmed the negligibly small interlayer coupling in MHMs. Unlike in previous single-layer measurements, two transmission peaks were observed for the double-layered MHM. Notably, by narrowing the interlayer spacing, the frequency difference between two distinct transmission peaks increased, and the transmission band widened. The number of transmission peaks is equal to the number of stacked MHM layers; the transmission peaks (except for the lowest frequency one) originate from the Fabry–Pérot resonances of the multilayered metamaterial slab (Supplementary Fig. 3). It can be predicted that a spectral transmission band will be formed by increasing the number of layers and that the corresponding transmission bandwidth will be determined directly by the interlayer spacing (Fig. 5). As can be seen for the measured and calculated range of spacing distances in Figs 4 and 5, the magnitude of optical activity is barely affected by the spacing distance because of negligible interlayer coupling. By stacking more layers, the polarization rotation can be increased linearly; for example, 135° for three layers and 180° for four layers. This spacing-independent optical activity is very desirable for manipulating the polarization because we could tailor the transmission bandwidth by varying the spacing without considering the interlayer effect on the magnitude of optical activity.
(a) Total transmission spectra for double-layered MHM, showing the results of experiments, FDTD simulation and the characteristic matrix method with different values of interlayer spacing s. (b) Corresponding polarization rotation and ellipticity with varying s. The red and blue dashed lines represent simulated polarization and ellipticity, respectively. The circles represent the corresponding experimental data. The following dimensions of interlayer spacing were tested: s=1.5, 3.0 and 5.0 mm.
Numerically calculated total transmission and polarization rotation as a function of the interlayer spacing for (a) three-layer-, (b) four-layer- and (c) five-layer MHMs. The solid and dashed lines represent the transmission spectra and polarization rotations, respectively. The metal was assumed to be a perfect electric conductor and no spacer was assumed to be inserted between the layers.
Discussion
We have shown that nondispersive optical activity can be realized with MHMs. This nonresonant property originates from the Drude-like response of MHMs. Since the thickness of a single-layer MHM is much smaller than the operating wavelength, MHMs can be utilized for broadband and ultrathin polarization manipulators. With the scaling behaviour of optical rotary power with respect to the thickness of the wire, the polarization rotation can be manipulated very easily, even with a single-layer MHM. Furthermore, the polarization rotation can be increased in proportion to the number of MHM layers, and the transmission bandwidth can be tailored by varying the interlayer spacing between the MHM layers. The proposed concept was validated experimentally in the microwave range; however, it is worth pointing out that the operating frequency could be shifted to a higher band by adjusting the size of the unit cell; for example, by utilizing modern nano/micro fabrication techniques such as direct laser writing24,51, MHMs that operate in the terahertz or far-infrared frequency ranges might be fabricated.
Methods
Sample fabrication
The supporting structure of the MHM was fabricated with an acrylic resin (EX200, 3D Systems) with commercial, layered-prototyping equipment (ProJet3000, 3D Systems) and coated with silver paste (P-100, Elcoat) for its metallic properties. The lateral dimensions of the structure were 170 × 170 mm.
Analytic descriptions for effective parameters
To qualitatively understand the frequency- and geometry-dependent effective parameters of MHMs, we calculate the induced polarization and magnetization resulting from the excitation of electromagnetic waves. For the sake of simplicity, the double helix structures that constituted the quadrants of the unit cell are assumed to be modelled with lumped inductance L and resistance R. In homogeneous electric and magnetic fields, the electric potential U is given by:

where S is the cross-sectional area of the helices defined as S=w1w2. Applying the effective RL circuit model, we have:

where the ± signs correspond to right- and left-handed double helix structure and Iw is the total current that flows through the metallic helices. Assuming the solution is time-harmonic, the formula for the total current can be obtained as:

From equation (6), the effective electric and magnetic dipole moments can be derived as follows:


where V0 is the volume of a unit cell and γ is the dissipation constant defined as R/L. Noting that D=ε0E+P, B=μ0H+μ0M and that the unit cell of MHM has a fourfold rotational symmetry, the average electric displacement and magnetic flux density under normal incidence can be derived as follows:


From equation (8) and the constitutive equation of general chiral media with reciprocity, the effective parameters of MHM can be assigned as follows:



where εb and μb are added for quantitative fitting of effective parameters (Supplementary Fig. 4).
Characterization of optical activity
The experiment was conducted with linearly polarized, broadband horn antennas and a network analyser to measure the scattering parameters. To characterize the MHM, polarization rotation and circular dichroism were estimated from the scattering parameters that were measured52. The magnitude of polarization rotation was calculated as  , where T is the complex transmission for the RCP (LCP) wave derived from co-polarized (Txx) and cross-polarized (Tyx) transmission coefficients, T±=Txx±iTyx. Circular dichroism can be characterized with the ellipticity
, where T is the complex transmission for the RCP (LCP) wave derived from co-polarized (Txx) and cross-polarized (Tyx) transmission coefficients, T±=Txx±iTyx. Circular dichroism can be characterized with the ellipticity  . In addition, the effective chirality parameter κ can be obtained as
. In addition, the effective chirality parameter κ can be obtained as  and
and  , where h is the thickness of the sample.
, where h is the thickness of the sample.
Additional information
How to cite this article: Park, H. S. et al. Nondispersive optical activity of meshed helical metamaterials. Nat. Commun. 5:5435 doi: 10.1038/ncomms6435 (2014).
References
Hallam, B. T., Lawrence, C. R., Hooper, I. R. & Sambles, J. R. Broad-band polarization conversion from a finite periodic structure in the microwave regime. Appl. Phys. Lett. 84, 849 (2004).
Duarte, F. J. Beam transmission characteristics of a collinear polarization rotator. Appl. Opt. 31, 3377–3378 (1992).
Azzam, R. M. A. Chiral thin solid films: method of deposition and applications. Appl. Phys. Lett. 61, 3118 (1992).
Pendry, J. B. A chiral route to negative refraction. Science 306, 1353–1355 (2004).
Zhang, C. & Cui, T. J. Negative reflections of electromagnetic waves in a strong chiral medium. Appl. Phys. Lett. 91, 194101 (2007).
Plum, E. et al. Metamaterial with negative index due to chirality. Phys. Rev. B 79, 035407 (2009).
Li, Z. et al. Chiral metamaterials with negative refractive index based on four “U” split ring resonators. Appl. Phys. Lett. 97, 081901 (2010).
Li, Z., Alici, K. B., Colak, E. & Ozbay, E. Complementary chiral metamaterials with giant optical activity and negative refractive index. Appl. Phys. Lett. 98, 161907 (2011).
Zhao, R., Zhang, L., Zhou, J., Koschny, T. & Soukoulis, C. M. Conjugated gammadion chiral metamaterial with uniaxial optical activity and negative refractive index. Phys. Rev. B 83, 035105 (2011).
Zarifi, D., Soleimani, M. & Nayyeri, V. A novel dual-band chiral metamaterial structure with giant optical activity and negative refractive index. J. Electromagn. Waves Appl. 26, 251–263 (2012).
Li, Z. et al. Composite chiral metamaterials with negative refractive index and high values of the figure of merit. Opt. Express 20, 6146–6156 (2012).
Song, K., Zhao, X. P., Fu, Q. H., Liu, Y. H. & Zhu, W. R. Wide-angle 90°-polarization rotator using chiral metamaterial with negative refractive index. J. Electromagn. Waves Appl. 26, 1967–1976 (2012).
Fedotov, V. et al. Asymmetric propagation of electromagnetic waves through a planar chiral structure. Phys. Rev. Lett. 97, 167401 (2006).
Fedotov, V. A., Schwanecke, A. S., Zheludev, N. I., Khardikov, V. V. & Prosvirnin, S. L. Asymmetric transmission of light and enantiomerically sensitive plasmon resonance in planar chiral nanostructures. Nano Lett. 7, 1996–1999 (2007).
Schwanecke, A. S. et al. Nanostructured metal film with asymmetric optical transmission. Nano Lett. 8, 2940–2943 (2008).
Menzel, C. et al. Asymmetric transmission of linearly polarized light at optical metamaterials. Phys. Rev. Lett. 104, 253902 (2010).
Huang, C., Feng, Y., Zhao, J., Wang, Z. & Jiang, T. Asymmetric electromagnetic wave transmission of linear polarization via polarization conversion through chiral metamaterial structures. Phys. Rev. B 85, 195131 (2012).
Zhao, R., Zhou, J., Koschny, T., Economou, E. & Soukoulis, C. Repulsive Casimir force in chiral metamaterials. Phys. Rev. Lett. 103, 103602 (2009).
Zhao, R., Koschny, T., Economou, E. N. & Soukoulis, C. M. Comparison of chiral metamaterial designs for repulsive Casimir force. Phys. Rev. B 81, 235126 (2010).
Zhang, W., Potts, A. & Bagnall, D. M. Giant optical activity in dielectric planar metamaterials with two-dimensional chirality. J. Opt. A Pure Appl. Opt. 8, 878–890 (2006).
Rogacheva, A. V., Fedotov, V. A., Schwanecke, A. S. & Zheludev, N. I. Giant gyrotropy due to electromagnetic-field coupling in a bilayered chiral structure. Phys. Rev. Lett. 97, 177401 (2006).
Bai, B., Svirko, Y., Turunen, J. & Vallius, T. Optical activity in planar chiral metamaterials: theoretical study. Phys. Rev. A 76, 023811 (2007).
Liu, N., Fu, L., Kaiser, S., Schweizer, H. & Giessen, H. Plasmonic building blocks for magnetic molecules in three-dimensional optical metamaterials. Adv. Mater. 20, 3859–3865 (2008).
Gansel, J. K. et al. Gold helix photonic metamaterial as broadband circular polarizer. Science 325, 1513–1515 (2009).
Zhukovsky, S. V, Novitsky, A. V & Galynsky, V. M. Elliptical dichroism: operating principle of planar chiral metamaterials. Opt. Lett. 34, 1988–1990 (2009).
Rockstuhl, C., Menzel, C., Paul, T. & Lederer, F. Optical activity in chiral media composed of three-dimensional metallic meta-atoms. Phys. Rev. B 79, 035321 (2009).
Ye, Y. & He, S. 90° Polarization rotator using a bilayered chiral metamaterial with giant optical activity. Appl. Phys. Lett. 96, 203501 (2010).
Xiong, X. et al. Construction of a chiral metamaterial with a U-shaped resonator assembly. Phys. Rev. B 81, 075119 (2010).
Decker, M., Zhao, R., Soukoulis, C. M., Linden, S. & Wegener, M. Twisted split-ring-resonator photonic metamaterial with huge optical activity. Opt. Lett. 35, 1593–1595 (2010).
Zhao, Y., Belkin, M. A. & Alù, A. Twisted optical metamaterials for planarized ultrathin broadband circular polarizers. Nat. Commun. 3, 870 (2012).
Hannam, K., Powell, D. A., Shadrivov, I. V. & Kivshar, Y. S. Dispersionless optical activity in metamaterials. Appl. Phys. Lett. 102, 201121 (2013).
Zhu, W., Rukhlenko, I. D., Huang, Y., Wen, G. & Premaratne, M. Wideband giant optical activity and negligible circular dichroism of near-infrared chiral metamaterial based on a complementary twisted configuration. J. Opt. 15, 125101 (2013).
Lagarkov, A. N. et al. Resonance properties of Bi-helix media at microwaves. Electromagnetics 17, 213–237 (1997).
Wu, C., Li, H., Wei, Z., Yu, X. & Chan, C. T. Theory and experimental realization of negative refraction in a metallic helix array. Phys. Rev. Lett. 105, 247401 (2010).
Gansel, J. K., Wegener, M., Burger, S. & Linden, S. Gold helix photonic metamaterials: a numerical parameter study. Opt. Express 18, 1059–1069 (2010).
Wu, C. et al. Metallic helix array as a broadband wave plate. Phys. Rev. Lett. 107, 177401 (2011).
Yang, Z. Y., Zhao, M., Lu, P. X. & Lu, Y. F. Ultrabroadband optical circular polarizers consisting of double-helical nanowire structures. Opt. Lett. 35, 2588–2590 (2010).
Li, S., Yang, Z., Wang, J. & Zhao, M. Broadband terahertz circular polarizers with single- and double-helical array metamaterials. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 28, 19–23 (2011).
Oh, S. S., Demetriadou, A., Wuestner, S. & Hess, O. On the origin of chirality in nanoplasmonic gyroid metamaterials. Adv. Mater. 25, 612–617 (2013).
Demetriadou, A., Oh, S. S., Wuestner, S. & Hess, O. A tri-helical model for nanoplasmonic gyroid metamaterials. New J. Phys. 14, 083032 (2012).
Yu, Y., Yang, Z., Li, S. & Zhao, M. Higher extinction ratio circular polarizers with hetero-structured double-helical metamaterials. Opt. Express 19, 10886–10894 (2011).
Zhao, Z. et al. High extinction ratio circular polarizer with conical double-helical metamaterials. J. Light Technol. 30, 2442–2446 (2012).
Yang, Z. et al. Polarization properties in helical metamaterials. Front. Optoelectron. 5, 248–255 (2012).
Bai, B., Ventola, K., Tervo, J. & Zhang, Y. Determination of the eigenpolarizations in arbitrary diffraction orders of planar periodic structures under arbitrary incidence. Phys. Rev. A 85, 053808 (2012).
Li, T. Q. et al. Magnetic resonance hybridization and optical activity of microwaves in a chiral metamaterial. Appl. Phys. Lett. 92, 131111 (2008).
Lapine, M., Shadrivov, I. V, Powell, D. a. & Kivshar, Y. S. Metamaterials with conformational nonlinearity. Sci. Rep. 1, 138 (2011).
Li, Z. et al. Coupling effect between two adjacent chiral structure layers. Opt. Express 18, 5375–5383 (2010).
Liu, N. & Giessen, H. Coupling effects in optical metamaterials. Angew. Chem. Int. Ed. 49, 9838–9852 (2010).
Born, M. & Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light CUP Archive (1999).
Wood, B., Pendry, J. & Tsai, D. Directed subwavelength imaging using a layered metal-dielectric system. Phys. Rev. B 74, 115116 (2006).
Rill, M. S. et al. Photonic metamaterials by direct laser writing and silver chemical vapour deposition. Nat. Mater. 7, 543–546 (2008).
Wang, B., Zhou, J., Koschny, T., Kafesaki, M. & Soukoulis, C. M. Chiral metamaterials: simulations and experiments. J. Opt. A Pure Appl. Opt. 11, 114003 (2009).
Acknowledgements
This work was supported by Basic Science Research Program (2012R1A2A1A03670391), Nano·Material Technology Development Program (2014039957), Global Frontier Program (2014M3A6B3063709), Pioneer Research Center Program (2014M3C1A3052537) and Quantum Metamaterials Research Center Program (2008-0061893) through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, and the World Class Institute (WCI) Program of the National Research Foundation of Korea (NRF) funded by the Korea government (WCI 2011-001).
Author information
Authors and Affiliations
Contributions
H.S.P., T.-T.K. and B.M. conceived the original idea. H.S.P. performed the numerical simulation and the microwave measurement. H.S.P., H.-D.K. and K.K. fabricated the samples. All the authors analysed the data and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-4. (PDF 1099 kb)
Rights and permissions
About this article
Cite this article
Park, H., Kim, TT., Kim, HD. et al. Nondispersive optical activity of meshed helical metamaterials. Nat Commun 5, 5435 (2014). https://doi.org/10.1038/ncomms6435
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms6435
This article is cited by
-
Double-use linear polarization convertor using hybrid metamaterial based on VO2 phase transition in the terahertz region
Applied Physics A (2018)
-
A terahertz in-line polarization converter based on through-via connected double layer slot structures
Scientific Reports (2017)
-
Broadband angle- and permittivity-insensitive nondispersive optical activity based on planar chiral metamaterials
Scientific Reports (2017)
-
Linearly Polarized Converters for Reflected and Transmitted Waves Based on Double-Split Ring Resonator
Plasmonics (2017)
-
Controllable optical activity with non-chiral plasmonic metasurfaces
Light: Science & Applications (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

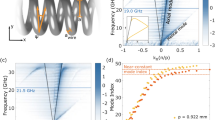


 is shown. (b) Numerically- and experimentally retrieved chirality parameter κ fitted to the analytic model. (c) Nondispersive polarization rotation and (d) nearly-zero ellipticity are shown.
is shown. (b) Numerically- and experimentally retrieved chirality parameter κ fitted to the analytic model. (c) Nondispersive polarization rotation and (d) nearly-zero ellipticity are shown.

