Abstract
Matter-wave interferometry performed with massive objects elucidates their wave nature and thus tests the quantum superposition principle at large scales. Whereas standard quantum theory places no limit on particle size, alternative, yet untested theories—conceived to explain the apparent quantum to classical transition—forbid macroscopic superpositions. Here we propose an interferometer with a levitated, optically cooled and then free-falling silicon nanoparticle in the mass range of one million atomic mass units, delocalized over >150 nm. The scheme employs the near-field Talbot effect with a single standing-wave laser pulse as a phase grating. Our analysis, which accounts for all relevant sources of decoherence, indicates that this is a viable route towards macroscopic high-mass superpositions using available technology.
Similar content being viewed by others
Introduction
Matter-wave interference with particles of increasing size and mass is a natural and viable method for testing the validity of the quantum superposition principle at unprecedented macroscopic scales1,2,3,4. Macroscopic path separations are nowadays routinely achieved in atom interferometry5,6,7, and technological advances in the control of opto-mechanical systems8 promise that much more massive objects may be delocalized9,10,11,12,13, albeit with spatial separations smaller than a single atom.
Recent proposals put forward nanoparticle interferometry14,15 in the mass range of 106–109 AMU to surpass the mass records currently held by molecule diffraction experiments3,16, while maintaining spatial separations large enough to be resolved by optical means. A first demonstration with molecular clusters15 is still far away from the mentioned high-mass regime due to difficult experimental challenges, mainly concerning the source and detection. The realization of a proposed double-slit scheme with silica nanospheres14 requires motional ground-state cooling, which is an equally challenging task.
Quite recently, optical feedback cooling has been demonstrated for 100-nm-sized particles17,18, based on pioneering work that demonstrated the trapping of polystyrene and glass microspheres19, trapping of viruses and bacteria20 and even of complete cells21 in solutions and high vacuum. Cavity cooling of particles of similar size was proposed22 and recently achieved23,24 in one dimension, with temperatures in the milli-Kelvin range. Although this is still far above the ground state of a typical 100-kHz trap, we will argue that high-mass interference can be realized experimentally with motional temperatures already achieved by optical cooling.
In this paper, we present a near-field interference scheme for 106 AMU particles. It is based on the single-source Talbot effect25 due to a single optical phase grating, as opposed to the three-grating scenario in Talbot–Lau interference experiments3. Optically trapped silicon nanospheres, feedback-stabilized to a thermal state of about 20 mK, provide a sufficiently coherent source. Individual particles are dropped and diffracted by a standing UV laser wave, such that interference of neighbouring diffraction orders produces a resonant near-field fringe pattern. In order to record the interferogram, the nanospheres are deposited on a glass slide and their arrival positions are recorded via optical microscopy. We argue that the choice of silicon, due to its specific material characteristics, will yield reliable high-mass interference, unaffected by environmental decoherence, in a set-up that can be realized with present-day technology.
Results
Proposed experiment
The proposed scheme is sketched in Fig. 1. In the first stage of the experiment, a silicon particle is captured in an optical dipole trap by a lens system of numerical aperture 0.8 focusing a 1,550 nm laser to a waist of 860 nm (ref. 26); the interaction of nanoparticles with light is described further in Supplementary Note 1. The trapping light is collected and used to determine the position of the particle18, which is feedback cooled over many trapping cycles to about T=20 mK of mean translational energy along the horizontal x-axis, implying a momentum uncertainty  of about σp/m=1.2 cm s−1. A laser power of 55 mW results in a trap frequency of νM=200 kHz and a position uncertainty σx <10 nm; see Supplementary Note 2. The trap thus serves as a nearly point-like matter-wave source for diffraction.
of about σp/m=1.2 cm s−1. A laser power of 55 mW results in a trap frequency of νM=200 kHz and a position uncertainty σx <10 nm; see Supplementary Note 2. The trap thus serves as a nearly point-like matter-wave source for diffraction.
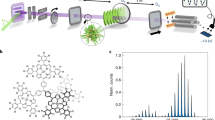
(a) Laser light at 1,550 nm creates a harmonic trap for single-silicon nanospheres. After feedback cooling to 20 mK, the particle is released and falls for 125 mm, where it passes a phase grating (b) provided by a retro-reflected nanosecond pulse at 355 nm. 275 mm further down the particle is adsorbed on a glass slide (c), where the arrival position is recorded with 100 nm accuracy via optical microscopy (d).
After feedback cooling, the particle is released from the trap and falls for t1=160 ms before it is illuminated by a frequency-trippled Nd:YAG laser pulse at 355 nm with a pulse length of 10 ns and an energy EG≤500 μJ. The pulse is retro-reflected by a mirror to form a standing-wave phase grating with period d=λG/2, which diffracts the particle by modulating the matter-wave phase through the dipole interaction. The Talbot time, which sets the scale for near-field interference3, is thus given by tT=md2/h≈80 ms. The laser beam must be expanded such that the waist is larger than the uncertainty in position σpt1/m≈2 mm accrued during free flight. Moreover, the orientation of the grating must be angularly stable to less than micro-radians to avoid blurring of the interferogram due to acceleration of the particle under gravity, and positionally stable to within 30 nm relative to the initial particle position; see Supplementary Note 3.
After the grating, the particle undergoes free fall for t2=126 ms, forming an interference pattern when it arrives on the glass slide. The arrival position can be detected by absorption imaging with visible light. Fitting to the known point-spread function of the imaging system permits 100 nm positional accuracy27; see Supplementary Note 4. The density pattern depicted in Fig. 2a is predicted to appear after many runs of the experiment. In the following, we discuss the theoretical description of the interference effect and the experimental constraints.
(a) Quantum and (b) classical probability densities at different times t2 after the grating pulse. We assume the width of the trap state to be σx=10 nm and a time of flight to the grating of t1=160 ms; the grating has the period d=177 nm with the maximal phase modulation set to φ0=π. The interference pattern is detected after t2=126 ms in the set-up of Fig. 1. Quantum mechanics then predicts high-contrast fringes, which cannot be explained classically.
Theoretical model
Our starting point for evaluating the interference effect is the trapped thermal state of motion, a Gaussian mixture with standard deviations  and
and  . The particle will be illuminated by a uniform standing-wave pulse oriented along the horizontal x-axis (see Fig. 1), so that the y- and z-motion can be ignored.
. The particle will be illuminated by a uniform standing-wave pulse oriented along the horizontal x-axis (see Fig. 1), so that the y- and z-motion can be ignored.
The near-field diffraction effect including all relevant decoherence mechanisms is best captured in a quantum phase-space description28. For the present purposes it is most useful to work with the characteristic function representation χ(s, q), that is, the Fourier transform of the Wigner function29 of a given quantum state ρ. Here, we summarize the detailed derivation given in Supplementary Methods. The initial Gaussian state,

first evolves freely for a time t1, χ1(s, q)=χ0(s−qt1/m, q), before it is illuminated by the optical grating pulse of period d. Given an almost point-like initial spread σx/d≪1, the matter waves must evolve for at least the Talbot time tT to ensure that they are delocalized over adjacent grating nodes in order to be able to interfere. The initial momentum, on the other hand, is spread over many grating momenta, σpd/h>>1, so that the time-evolved state extends over many grating periods. That is, if particles are only detected in a finite detection window around the centre of the distribution in the end, we can neglect the Gaussian density profile by writing

The particle interacts with the standing-wave pulse through its optical polarizability  , determined by the particle radius R and its complex refractive index nSi at the grating wavelength λG=2d. In the limit of short pulse durations τ, this imprints the phase φ(x)=φ0 cos2(πx/d) on the matter-wave state15, where φ0=2Re(α)EG/ħcε0aG depends on the energy EG and spot area aG of the pulse. The characteristic function transforms as
, determined by the particle radius R and its complex refractive index nSi at the grating wavelength λG=2d. In the limit of short pulse durations τ, this imprints the phase φ(x)=φ0 cos2(πx/d) on the matter-wave state15, where φ0=2Re(α)EG/ħcε0aG depends on the energy EG and spot area aG of the pulse. The characteristic function transforms as  , where the Bn are Talbot coefficients, given in terms of Bessel functions30,
, where the Bn are Talbot coefficients, given in terms of Bessel functions30,

Incoherent effects due to absorption or scattering of laser photons are negligible for the nanoparticles considered here (Supplementary Methods); nevertheless, our numerical simulations include both effects.
The final density distribution w(x)=‹x|ρ|x›, that is, the probability to find the particle at position x after another free time evolution by t2, then takes the form

It describes a periodic fringe pattern oscillating at the geometrically magnified grating period D=d(t1+t2)/t1 (ref. 25). The fringe amplitudes, given by the Talbot coefficients (3), are diminished the larger the spread σx of the initial state (1).
An exemplary density pattern (4) is plotted in Fig. 2a for varying time t2. The simulation was performed for 106 AMU silicon particles, assuming realistic experimental parameters and including the influence of environmental decoherence. It shows pronounced interference fringes with visibilities of up to 75%.
The pattern in Fig. 2b is the result of a classical simulation assuming that the particles are moving on ballistic trajectories. A lensing effect due to the strong dipole forces exerted by the standing-wave field is here responsible for the density modulation. This classical result is obtained simply by replacing sin πξ by πξ in expression (3) for the grating coefficients30.
The clear difference between the quantum and the classical pattern is captured by the sinusoidal fringe visibility, the ratio between the amplitude and the offset of a sine curve of period D fitted to the density pattern (4):

As shown in Fig. 3, the classical and the quantum prediction differ significantly: the classical theory predicts many regions of low contrast as a function of φ0, whereas the quantum prediction exhibits a slow φ0 dependence. The highest quantum visibility amounts to 83% at φ0=1.4π.
Accounting for decoherence
A realistic assessment of the proposed scheme must also include the influence of collisional and thermal decoherence28. This is incorporated into (4) by multiplying each Fourier component with a reduction factor of the form

where Γ gives the rate and f(x) determines the spatial resolution of decoherence events of a certain class. In our simulation we accounted for collisions with residual gas particles, scattering and absorption of blackbody photons, and thermal emission of radiation using a realistic microscopic description. Each process contributes another factor Rn listed in the Supplementary Methods; the rate of thermal emission depends on time since the particle loses internal energy and cools during flight.
Experimental constraints
As a major concern for the successful implementation of the experiment, environmental decoherence must be kept sufficiently low. According to our simulations, collisional decoherence can be essentially avoided at ultra-high vacuum pressures of 10−10 mbar.
Radiative decoherence is suppressed by choosing silicon spheres because they are essentially transparent at typical wavelengths of room temperature blackbody radiation. The thermal emission of photons is determined by the internal temperature of the nanospheres, which is set in the trapping stage of the experiment. A trapping intensity of 90 mW μm−2 leads to an initial heating rate ∂tTint=200 K s−1 and an equilibrium temperature of 1,600 K. This high value is a consequence of the low blackbody emissivity of silicon31, implying that the particle does not lose heat efficiently while in the trap. Nevertheless, due to the high refractive index nSi=3.48 of silicon, the particle may be trapped for well in excess of a second before the temperature rises that high. This time corresponds to about 105 trap oscillations, a sufficient period to perform parametric feedback cooling of the motion to T=20 mK; see Supplementary Note 5. The low emissivity of silicon is the essential advantage compared to other materials such as silica, for which much work in this field has been done10,11,23. We find that to perform this experiment with silica would require cryogenic cooling of both apparatus and nanoparticle to 100 K, whereas thermal decoherence of silicon becomes important only at internal temperatures in excess of 1,000 K. Moreover, the high refractive index of silicon compared to the value nSiO2=1.44 of silica means that less optical power is required to trap the sphere and to monitor its position24.
As an additional advantage, silicon absorbs strongly at optical frequencies, which simplifies the detection of the interferogram. In principle, this would also affect the interaction with the grating laser, since a particle at the anti-node of the grating absorbs on average n0=0.12φ0 photons. For a grating laser waist of 30 mm we anticipate a phase modulation of φ0/EG=50 rad mJ−1 and hence we can access φ0≤4π. The finite absorption of grating photons, which is included in the simulations, disturbs the interferogram little.
Discussion
We presented a viable scheme for high-mass nanoparticle interferometry, which employs only a single optical diffraction element and requires only moderate motional cooling. The set-up would operate in ultra-high vacuum at room temperature. It is limited to masses up to 106 AMU mainly by the growing Talbot time and free-fall distance32. Interferometry in a microgravity environment could pave the way to even higher masses33.
Remarkably, with path separations of up to 150 nm and interrogation times of 300 ms, the presented scheme is already sensitive to alternative theories beyond the Schrödinger equation. The renowned collapse model of continuous spontaneous localization (CSL)34 could be probed in its current formulation4. In fact, a successful demonstration of interference with a visibility exceeding 42% would bound the localization rate to λCSL<1.4 × 10−11 Hz, a value at the lower end of recent estimates for this parameter35,36; see Supplementary Discussion. Such a superposition experiment can be associated with a macroscopicity value of μ=18 (ref. 37), substantially exceeding that of every present-day matter-wave experiment and comparing well with the most ambitious micromirror superposition proposals9.
Additional information
How to cite this article: Bateman, J. et al. Near-field interferometry of a free-falling nanoparticle from a point-like source. Nat. Commun. 5:4788 doi: 10.1038/ncomms5788 (2014).
References
Clauser, J. inExperimental Metaphysics (eds Cohen R. S., Horne M., Stachel J. 1–11Kluwer Academic (1997).
Leggett, A. J. Testing the limits of quantum mechanics: motivation,state of play, prospects. J. Phys.: Condens. Matter 14, R415 (2002).
Hornberger, K., Gerlich, S., Haslinger, P., Nimmrichter, S. & Arndt, M. Colloquium: quantum interference of clusters and molecules. Rev. Mod. Phys. 84, 157 (2012).
Bassi, A., Lochan, K., Satin, S., Singh, T. P. & Ulbricht, H. Models of wave-function collapse, underlying theories, and experimental tests. Rev. Mod. Phys. 85, 471–527 (2013).
Müller, H., Chiow, S.-w., Long, Q., Herrmann, S. & Chu, S. Atom interferometry with up to 24-photon-momentum-transfer beam splitters. Phys. Rev. Lett. 100, 180405 (2008).
Müntinga, H. et al. Interferometry with Bose-Einstein condensates in microgravity. Phys. Rev. Lett. 110, 093602 (2013).
Dickerson, S. M., Hogan, J. M., Sugarbaker, A., Johnson, D. M. S. & Kasevich, M. A. Multiaxis inertial sensing with long-time point source atom interferometry. Phys. Rev. Lett. 111, 083001 (2013).
Aspelmeyer, M., Kippenberg, T. J. & Marquardt, F. Cavity Optomechanics. Preprint at arXiv:1303.0733 (2013).
Marshall, W., Simon, C., Penrose, R. & Bouwmeester, D. Towards quantum superpositions of a mirror. Phys. Rev. Lett. 91, 130401 (2003).
Chang, D. et al. Cavity opto-mechanics using an optically levitated nanosphere. Proc. Natl Acad. Sci. USA 107, 1005–1010 (2010).
Romero-Isart, O., Juan, M. L., Quidant, R. & Cirac, J. I. Toward quantum superposition of living organisms. New J. Phys. 12, 033015 (2010).
Scala, M., Kim, M. S., Morley, G. W., Barker, P. F. & Bose, S. Matter-wave interferometry of a levitated thermal nano-oscillator induced and probed by a spin. Phys. Rev. Lett. 111, 180403 (2013).
Yin, Z.-q., Li, T., Zhang, X. & Duan, L. Large quantum superpositions of a levitated nanodiamond through spin-optomechanical coupling. Phys. Rev. A 88, 033614 (2013).
Romero-Isart, O. et al. Large quantum superpositions and interference of massive nanometer-sized objects. Phys. Rev. Lett. 107, 020405 (2011).
Nimmrichter, S., Haslinger, P., Hornberger, K. & Arndt, M. Concept of an ionizing time-domain matter-wave interferometer. New J. Phys. 13, 075002 (2011).
Eibenberger, S., Gerlich, S., Arndt, M., Mayor, M. & Tüxen, J. Matter-wave interference with particles selected from a molecular library with masses exceeding 10,000 amu. Phys. Chem. Chem. Phys. 15, 14696–14700 (2013).
Li, T., Kheifets, S. & Raizen, M. Millikelvin cooling of an optically trapped microsphere in vacuum. Nat. Phys. 7, 527–530 (2011).
Gieseler, J., Deutsch, B., Quidant, R. & Novotny, L. Subkelvin parametric feedback cooling of a laser-trapped nanoparticle. Phys. Rev. Lett. 109, 103603 (2012).
Ashkin, A., Dziedzic, J., Bjorkholm, J. & Chu, S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt. Lett. 11, 288–290 (1986).
Ashkin, A. & Dziedzic, J. Optical trapping and manipulation of viruses and bacteria. Science 235, 1517–1520 (1987).
Ashkin, A., Dziedzic, J. & Yamane, T. Optical trapping and manipulation of single cells using infrared laser beams. Nature 330, 769–771 (1987).
Barker, P. Doppler cooling a microsphere. Phys. Rev. Lett. 105, 073002 (2010).
Kiesel, N. et al. Cavity cooling of an optically levitated nanoparticle. Proc. Natl Acad. Sci. USA 110, 14180–14185 (2013).
Asenbaum, P., Kuhn, S., Nimmrichter, S., Sezer, U. & Arndt, M. Cavity cooling of free silicon nanoparticles in high vacuum. Nat. Commun. 4, 2743 (2013).
Brezger, B., Arndt, M. & Zeilinger, A. Concepts for near-field interferometers with large molecules. J. Opt. B. 5, S82 (2003).
Richards, B. & Wolf, E. Electromagnetic diffraction in optical systems. II. Structure of the image field in an aplanatic system. Proc. R. Soc. Lond. A 253, 358–379 (1959).
Hell, S. W. Far-field optical nanoscopy. Science 316, 1153 (2007).
Hornberger, K., Sipe, J. & Arndt, M. Theory of decoherence in a matter wave Talbot-Lau interferometer. Phys. Rev. A 70, 053608 (2004).
Schleich, W. P. Quantum Optics in Phase Space Wiley-VCH (2001).
Hornberger, K. et al. Theory and experimental verification of Kapitza—Dirac—Talbot—Lau interferometry. New J. Phys. 11, 043032 (2009).
Palik, E. D. & Ghosh, G. Handbook of Optical Constants of Solids: Five-Volume Set Academic Press (1998).
Nimmrichter, S., Hornberger, K., Haslinger, P. & Arndt, M. Testing spontaneous localization theories with matter-wave interferometry. Phys. Rev. A 83, 043621 (2011).
Kaltenbaek, R. et al. Macroscopic quantum resonators (MAQRO). Exp. Astron. 34, 123–164 (2012).
Ghirardi, G. C., Pearle, P. & Rimini, A. Markov processes in Hilbert space and continuous spontaneous localization of systems of identical particles. Phys. Rev. A 42, 78 (1990).
Adler, S. L. Lower and upper bounds on CSL parameters from latent image formation and IGM heating. J. Phys. A 40, 2935 (2007).
Bassi, A., Deckert, D.-A. & Ferialdi, L. Breaking quantum linearity: constraints from human perception and cosmological implications. Europhys. Lett. 92, 50006 (2010).
Nimmrichter, S. & Hornberger, K. Macroscopicity of mechanical quantum superposition states. Phys. Rev. Lett. 110, 160403 (2013).
Acknowledgements
Funding by the EPSRC (EP/J014664/1), the Foundational Questions Institute (FQXi) through a Large Grant, and by the John F Templeton foundation (grant 39530) is gratefully acknowledged. This work was also partially supported by the European Commission within NANOQUESTFIT (No. 304886).
Author information
Authors and Affiliations
Contributions
H.U. conceived the interferometer and initiated the research. J.B. and S.N. designed the scheme and performed calculations and simulations. K.H. advised on the theory. All authors discussed the results and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-5, Supplementary Notes 1-5, Supplementary Discussion, Supplementary Methods and Supplementary References (PDF 935 kb)
Rights and permissions
About this article
Cite this article
Bateman, J., Nimmrichter, S., Hornberger, K. et al. Near-field interferometry of a free-falling nanoparticle from a point-like source. Nat Commun 5, 4788 (2014). https://doi.org/10.1038/ncomms5788
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms5788
This article is cited by
-
Present status and future challenges of non-interferometric tests of collapse models
Nature Physics (2022)
-
A way forward for fundamental physics in space
npj Microgravity (2022)
-
Stroboscopic high-order nonlinearity for quantum optomechanics
npj Quantum Information (2021)
-
Testing the foundation of quantum physics in space via Interferometric and non-interferometric experiments with mesoscopic nanoparticles
Communications Physics (2021)
-
Quantum control of a nanoparticle optically levitated in cryogenic free space
Nature (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.