Abstract
Random walks on networks is the standard tool for modelling spreading processes in social and biological systems. This first-order Markov approach is used in conventional community detection, ranking and spreading analysis, although it ignores a potentially important feature of the dynamics: where flow moves to may depend on where it comes from. Here we analyse pathways from different systems, and although we only observe marginal consequences for disease spreading, we show that ignoring the effects of second-order Markov dynamics has important consequences for community detection, ranking and information spreading. For example, capturing dynamics with a second-order Markov model allows us to reveal actual travel patterns in air traffic and to uncover multidisciplinary journals in scientific communication. These findings were achieved only by using more available data and making no additional assumptions, and therefore suggest that accounting for higher-order memory in network flows can help us better understand how real systems are organized and function.
Similar content being viewed by others
Introduction
A central objective of network science is to connect structure with dynamics in integrated social and biological systems1,2,3,4. In this data-driven approach, the complex structure is represented with a network of nodes and links, and the dynamics are modelled with random flow on the network5,6,7,8,9. The flow can represent ideas circulating among colleagues, passengers travelling through airports or patients moving between hospital wards. Conventional network models implicitly assume that where the flow moves to only depends on where it is, and that this first-order Markov process suffices for performing community detection, ranking and spreading analysis. Shannon10 introduced higher-order memory models in 1948, and there is a substantial body of work on analysing memory effects in, for example, time-series analysis for forecasting financial markets11, correlated random walks for predicting animal movements12 and exponential random graph models for capturing social networks13. Moreover, there is recent evidence that memory is necessary for accurately predicting web traffic14,15, for improving search and navigation in information networks16,17,18 and for capturing important phenomena in the spread of information19,20,21,22,23 and epidemics24,25,26,27,28,29. Nevertheless, little is known about memory effects on community detection, ranking and spreading analysis, three principal methods in network science. This issue raises a fundamental question that allows us to better understand social and biological systems: what are the effects of ignoring higher-order memory in network flows on community detection, ranking and spreading?
To comprehend the effects of memory, we use networks in which the direction of flow depends on the weights of the outgoing links and, importantly, where the flow comes from. In this study, we focus on second-order Markov dynamics such that the next step depends on the currently and previously visited node, which corresponds to a second-order Markov model of flow. As an illustration, we use air traffic between airports of different cities with link weights derived from real itineraries (Fig. 1). When we take first-order Markov dynamics into account in the conventional network approach, nodes i represent cities and links i→j represent flight legs, with weights W(i→j) proportional to the passenger volume between cities. The dynamics are modelled with weighted steps between nodes on networks without memory and correspond to a first-order Markov model of flow, as the direction of flow only depends on the currently visited city (Fig. 1a). This conventional approach is used in a wide range of problems, from ranking nodes6 and finding communities30,31 to modelling the spread of epidemics32,33 and rumours34. However, this approach ignores where the passengers come from, and therefore the direction of passenger flow is independent of the incoming traffic. When we take second-order Markov dynamics into account, on the other hand, memory nodes  represent flight legs and links
represent flight legs and links  represent connected flight legs, with weights
represent connected flight legs, with weights  proportional to the passenger volume between cities and conditional on the previously visited city. In this way, a city is represented by a physical node j with multiple memory nodes , one for each incoming flight leg from city i, such that arriving in Chicago from Seattle corresponds to arriving at memory node Seattle Chicago of physical node Chicago. By modelling the dynamics on this network with memory, such that steps depend on the currently and previously visited city, we can better reveal actual travel patterns (Fig. 1b).
proportional to the passenger volume between cities and conditional on the previously visited city. In this way, a city is represented by a physical node j with multiple memory nodes , one for each incoming flight leg from city i, such that arriving in Chicago from Seattle corresponds to arriving at memory node Seattle Chicago of physical node Chicago. By modelling the dynamics on this network with memory, such that steps depend on the currently and previously visited city, we can better reveal actual travel patterns (Fig. 1b).
(a) In a first-order Markov approach, we model passengers’ travel to a city to be proportional to the observed volume of traffic to that city, and irrespective of where the passengers come from. (b) In a second-order Markov model, passengers’ travel to a city is still proportional to the traffic volume, but also dependent on where the passengers come from. In this example, out-and-back traffic to Chicago only dominates overtransfer traffic when second-order Markov dynamics are taken into account. (c,d) Journal citation flow shows the same memory effect. Citation flow from four different journals to PNAS is mostly shown to return to the same journal or continue to a related journal only when second-order Markov dynamics are taken into account. The percentages represent the relative return flow.
Although we considered passengers moving between cities in this illustration, we have analysed six diverse systems in detail, including researchers navigating between journals and patients moving between wards. We find that taking second-order Markov dynamics into account is important for understanding the actual dynamics, because random dynamics on networks obscure essential structural information. After deriving how we model the dynamics and quantify their constraints, we show how the second-order Markov constraints on dynamics influence three important branches of network science: community detection, ranking and epidemic spreading.
Results
Modelling second-order Markov dynamics
For each system, we model the dynamics as a stochastic process. We represent the n different components of the system with physical nodes i =1,2,…,n and let Xt denote the state or position of an entity of flow at time t. With this notation, the flow through the system corresponds to a walker stepping between nodes, which can be described by an indexed sequence of random variables X1X2…Xt. In general, the probability that the flow visits node i at time t + 1 depends on the full history of the dynamic process:

for all i1,i2,…,it,it+1εi = 1,2,…,n. In network science, it is common to assume that the direction flow takes in a dynamic process depends only on the current state and not on time:

In other words, the dynamic process is Markovian or a first-order Markov process (M1), that is, it is assumed that knowledge about the relative weights of links between the nodes is sufficient to model the dynamic process in the system. All this information is captured in the transition matrix P with elements of the form

measuring the probability that a random walker at node i steps to node j and normalized such that ∑j p(i → j)=1. Accordingly, the probability of finding the random walker at node j at time t+1 is

Many ranking6,35 and community detection30,31 methods, as well as epidemic models9 build directly on this first-order Markov process. In fact, also maximal-entropy random walks are Markovian, although they build on modified transition probabilities36,37.
As we argue below, random dynamics on networks cannot accurately capture empirical flow pathways. As a result, a first-order Markov modelling can fail to capture important phenomena in a broad range of complex systems32,33. To capture higher-order Markov effects in flow pathways24,26,27,28, we use memory networks. A memory network consists of memory nodes; each memory node represents the current state of the walker, the currently visited node and the previous step or steps. The order of the Markov process determines the number of steps that represent a state. For example, in a second-order Markov process (M2), the walker’s next step depends on the currently visited node j and the previously visited node i. In this case, the memory nodes  correspond to directed links between physical nodes in the standard network. Accordingly, the network of memory nodes is a form of line graph of the network without memory (see Supplementary Note 1). In a third-order Markov process, the walker’s next step depends on the currently visited node j and the two previously visited nodes h and i, and the memory nodes
correspond to directed links between physical nodes in the standard network. Accordingly, the network of memory nodes is a form of line graph of the network without memory (see Supplementary Note 1). In a third-order Markov process, the walker’s next step depends on the currently visited node j and the two previously visited nodes h and i, and the memory nodes  correspond to three-step pathways between physical nodes in the standard network. Here we focus on a second-order Markov process, but the procedure can in principle easily be generalized to higher-order Markov processes, provided that sufficient data are available to fit the model.
correspond to three-step pathways between physical nodes in the standard network. Here we focus on a second-order Markov process, but the procedure can in principle easily be generalized to higher-order Markov processes, provided that sufficient data are available to fit the model.
The dynamics of a second-order Markov walker can now simply be modelled as a Markov process on the memory network, instead of a non-Markov process on the physical nodes. For a second-order Markov process, the dynamics are encoded by a transition matrix with elements of the form

measuring the probability that the walker steps from j to k if it came from i in the previous step and normalized such that  . These transitions can therefore be interpreted as movements between links. However, even in undirected networks, we must use two memory nodes for each pair of connected nodes i and j, as the memory nodes encode the time ordering of the visits. In any case, the probability of finding the random walker at memory node
. These transitions can therefore be interpreted as movements between links. However, even in undirected networks, we must use two memory nodes for each pair of connected nodes i and j, as the memory nodes encode the time ordering of the visits. In any case, the probability of finding the random walker at memory node  at time t+1 is
at time t+1 is

Consequently, the probability of finding the random walker at physical node k at time t+1 in a second-order Markov process is

Constraints on flow captured in real-world pathway data
We collected pathway data with sequences of steps for the six well-studied and diverse systems presented in Table 1: flight itineraries between US airports, the airports aggregated in cities, chains of citing articles aggregated in journals, movements of patients between hospital wards in Stockholm, GPS-tracked taxis in San Francisco and chains of forwarded and replied emails (see Supplementary Note 1). We chose these systems because their pathway data were readily available and because the outcomes of their analyses have important consequences. To explain the effects of memory, we analysed the systems with networks with and without memory.
The pathways in Fig. 1 illustrate how second-order Markov dynamics strongly direct flow in two real-world examples. With data from actual itineraries, Fig. 1a,b show trips to/from Chicago modelled with first-order Markov dynamics in a and with second-order Markov dynamics in b (see Methods). When only the relative proportions of departures from Chicago determines the next destination in the standard network representation, the trips mix randomly. With a second-order Markov model, however, passengers flying to Chicago are most likely to return to the city from which they came. Similarly, Fig. 1c,d show the journal citation flow to/from the journal PNAS with first-order Markov dynamics in c and with second-order Markov dynamics in d. The journal citation flow is a proxy for how researchers navigate scholarly literature, derived from a random walker moving between articles following citations and mapped onto journals. When only the fraction of citations from PNAS to the specialized journals determines which journal the walker reads next, the pathways mix randomly. Instead, with second-order Markov dynamics taken into account, after following a citation in an article published in a more specialized journal to an article in PNAS, the walker tends to return to an article published in the same specialized journal or field. Defined as the relative amount of flow that returns to the same physical node after two steps, the two-step return rate is twice as large when second-order Markov dynamics is accounted for in citation flow and eight times as large in passenger flow. Except for the taxi data (taxis take us to destinations away from where we were), we found that second-order Markov dynamics reveal a dramatically higher return flow in all studied systems (Table 1).
To quantify the second-order Markov constraints on flow, we measured the entropy rate of a random walker on a network with and without memory10. The entropy rate measures the conditional entropy, the uncertainty of the next step of the flow given the current state, weighted by the stationary distribution. In a first-order Markov process, the entropy rate is the conditional entropy at each physical node weighted by the stationary distribution:

where π is the stationary solution of the random process. In a second-order Markov process, the entropy rate is the conditional entropy at each memory node weighted by the stationary distribution:

The more effect memory has, the more the conditional entropy will decrease in the second-order Markov model. For the analysed networks, the entropy rates decrease by one to two bits when second-order Markov dynamics are taken into account (see Table 1). To put this decrease in perspective, we can compare with an unweighted network, in which the typical number of neighbours halves for each bit the entropy rate decreases. That is, were the links unweighted, the observed decrease in entropy rates would correspond to overestimating the effective number of neighbours by 200–400%. The nodes with the strongest memory effect have high entropy with first-order and low entropy with second-order Markov dynamics. For many nodes, memory greatly reduces the effective connectivity and reveals the constraints on flow (Fig. 2).
(a–f) First- and second-order conditional entropy for all nodes of the six analysed networks. Blue nodes show a significant memory effect, because the null hypothesis that the data are generated from a first-order Markov model can be rejected. Red nodes do not show a significant effect. The memory effect is the difference in entropy between a first- and second-order Markov model. Las Vegas, among all cities, shows the strongest memory effect. Traffic is dominated by visitors who return to the city from which they came. In the other extreme, nodes that we could not significantly distinguish from a first-order Markov model typically have low connectivity and relatively small entropies.
Second-order Markov constraints on flow are statistically significant. To verify that our results are based on sufficient data, we performed bootstrap resampling of pathways for all summary statistics and surrogate data testing of the entropy rate to estimate the Markov order38 (see Fig. 2, Methods and Supplementary Note 2). All summary statistics in Table 1 and a majority of influential nodes in all networks except patients and emails show a significant second-order Markov effect that cannot be explained by noise. Although we focus on second-order Markov dynamics in this paper, it is interesting to reflect on potential effects of higher-order Markov models. For example, a second-order Markov model captures real dynamics with one-step memory, including the two-step return rate, a third-order Markov model captures two-step memory, including the three-step return rate, and so on. In principle, we could go to any order n for higher accuracy. In practice, however, higher-order Markov models are more complex and demand many long pathways to statistically separate real effects of memory from insufficient data15. For the air-traffic data, we have enough long pathways to measure the entropy rate of a higher-order Markov model. When we estimated the average amount of information necessary to determine the next destination of passengers at airports, we measured a 0.3-bit decrease from second to third order compared with 1.1 bits from first to second order (see Supplementary Note 2 and Supplementary Fig. 3). Although both results are statistically significant according to a surrogate data test, this small difference suggests that a second-order Markov model captures most of the salient features set by the constraints on flow in air-traffic, namely, that passengers tend to return to the city from which they came.
We now turn to the consequences of ignoring higher-order memory when analysing network flows in social and biological systems. To study the consequences, we modified and generalized three commonly used network techniques to capture the effects of memory in a second-order Markov model: the map equation for community detection, PageRank for ranking and two compartmental models for spreading. We begin with community detection, as simplifying and highlighting important structures of the dynamics allow us to better understand and explain the effects of second-order Markov dynamics on ranking and spreading dynamics.
Memory affects community detection
We used the map equation framework to identify overlapping modules with long flow persistence times30,39 in networks with and without memory (see Methods and Supplementary Note 3). This information-theoretic method measures how efficient a modular description is in compressing the pathways of a random walker. The more structural information that can be exploited, the better the compression10. We measured how well modules identified with first- and second-order Markov dynamics can compress the more detailed model of the actual pathways (see Methods). Table 1 shows that second-order Markov dynamics allow for better compression, because random dynamics on networks obscure essential structural information. We quantified this structural information in terms of module size and level of module overlap. Measured as the average visit frequency of a random walker in each module, and weighted by the same visit frequency to reduce the effect of small modules, we report the effective module size for all networks in Table 1. Community detection of passenger traffic modelled as first-order Markov dynamics only identifies major geographic regions, such as the West, the South, the Mid-West and the East. Second-order Markov dynamics reveal much more detailed travel patterns and the typical module size is more than five times smaller. Analysing the hospital data, we found that patients are sent back to the previously visited ward more than half of the time, or more than three times as often as asserted by a standard network approach. As a result, the typical module within which patients move is significantly smaller when second-order Markov effects are taken into account. Memory also impacts information spreading through email communication. We found that the two-step return rate was four times higher with second-order Markov dynamics, thus revealing an organization with halved module sizes. We used the map equation framework, because it was straightforward to generalize its mathematics to second-order Markov dynamics, but the results are, in principle, universal for any method operating on the dynamics on a network31. The universality is manifested in the direct effect memory in network flows has on the spectral gap40,41. If memory favours spread across a system, the spectral gap increases and, the other way around, if memory confines flow, the spectral gap decreases. Overall, in the systems analysed here second-order Markov dynamics reveal a higher return flow that confines flow in smaller and more informative modules.
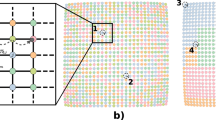
Memory affects the level of module overlap. In air traffic between US cities modelled with first-order Markov dynamics, both Las Vegas and Atlanta are assigned to a single major module, as shown in Fig. 3a, but second-order Markov dynamics reveal their different flow patterns. Atlanta, with many transferring passengers and a relatively low two-step return rate (15% with second-order and 1.8% with first-order Markov dynamics), is assigned to only one major module shown in red in Fig. 3b. In contrast, Las Vegas, with traffic dominated by returning tourists (67% two-step return rate with second-order and 3.7% with first-order Markov dynamics), is assigned to eight major modules, as shown in Fig. 3b (see Methods). Similarly, Supplementary Table 3 shows that second-order Markov dynamics can reveal multidisciplinary journals in the scholarly literature. For example, an ecologist reading an article published in PNAS will most probably next read an article published in an ecological journal, as shown in Fig. 1d and confirmed by the increased two-step and three-step return rates. This memory effect changes the perceived organization of the scholarly literature. With first-order Markov dynamics, PNAS is assigned to a single biological field. With second-order Markov dynamics, however, PNAS is assigned to five fields, including cell biology, ecology and mathematics. Likewise, the multidisciplinary journal Science is assigned to ten fields with second-order compared with one field with first-order Markov dynamics. Contrarily, field-specific journals, such as Ecology or Plant Cell, are clustered in single fields both with first- and second-order Markov dynamics. Measured as the average number of module assignments per physical node, we report the module assignments for all networks in Table 1. Compared with first-order Markov analysis in the systems analysed here, community detection with second-order Markov dynamics reveals system organizations with more and smaller modules that overlap to a greater extent.
The memory effects on community detection have interesting network-theoretical implications. Community-detection methods typically identify modules with stronger internal than external connections42,43 or with relatively long flow persistence times30,31. A problem with these methods is that they tend to assign each node to a very limited number of modules, in contrast to the observation that real modules often show pervasive overlap44,45,46. Rather than being a shortcoming of the algorithms, our results show that this problem can be a result of distorted modular dynamics in standard networks that prevent the methods from capturing the underlying dynamics and uncovering the actual modules, as with the air traffic example in Fig. 3. Interestingly, some heuristic algorithms for finding highly overlapping modules in standard networks can be seen as trying to account for second-order Markov dynamics (see Supplementary Note 3). The clique percolation47 and link clustering44 methods are known as topological methods that operate on the network structure without inducing flow on the links. If we take a flow perspective, the percolation of cliques can be seen as restricting flow to stay within connected cliques47. In addition, the coupling of links by neighbour similarity can be seen as prolonging flow persistence times in highly connected modules44. As we show in the Methods section, they are reasonably good at identifying overlapping communities of second-order dynamics aggregated in undirected standard networks. Nevertheless, using empirical data of flow pathways rather than clever assumptions has several advantages. Aggregating links in standard networks inevitably destroys information that cannot be fully recovered. As the benchmark test in Methods shows, a method that operates directly on the flow pathways can achieve superior results.
Memory affects ranking of nodes
When going from rankings based on counting links to measuring the average visit frequency of a random walker on a standard network,that is, calculating the PageRank6, the importance of neighbours becomes evident. Similarly, when going to PageRank on a network with second-order memory, the amount of flow received from neighbours also depends on the flow’s origin15,48. We define a generalized second-order PageRank as the stationary solution of equation (6)

Solving equation (6) requires finding the dominant eigenvector of the L × L transition matrix  , where L is the number of memory nodes. Note that this matrix is asymmetric even if the original network is undirected, as a transition
, where L is the number of memory nodes. Note that this matrix is asymmetric even if the original network is undirected, as a transition  does not exist in the opposite direction
does not exist in the opposite direction  , even if each link is bidirectional. After finding
, even if each link is bidirectional. After finding  , the centrality of physical nodes in the original network is given simply by
, the centrality of physical nodes in the original network is given simply by

where the second equality holds because of conservation of probability (see Methods for details on ergodicity).
To illustrate the effect of second-order Markov dynamics on ranking and on PageRank in particular, we focus on the journal citation network (see Supplementary Note 4 for analytical results). This example has practical applications because PageRank is a popular measure for ranking the scientific importance of journals49. In the citation network, we observe that 10% of the flow is re-allocated when moving from a first-order to a second-order Markov model (see Table 1). Some journals benefit from this re-allocation and some do not. The interesting question is: which ones gain and why?
Figure 4a shows why some journals increase their ranking from a first- to a second-order Markov model. For example, Ecology gains in total flow, which can primarily be explained by the amount of flow coming from high-quality journals (green), the amount of internal flow coming from journals without crossing community boundaries (dark blue) and the amount of flow returning after two steps (dark red). We consider high-quality flow to be the flow from the top ten journals. Flow from these journals comprises 1/3 of all flow in the system. For Ecology, there is an increase in return flow and internal flow when moving from a first- to a second-order Markov model, as well as a slight increase in flow from the top ten journals.
(a) Comparing changes in flow from a first- to a second-order Markov model (M1 to M2). Three kinds of flow were tracked for all journals in both M1 and M2: (1) quality flow from the top ten journals (green) or all other journals (yellow), (2) internal flow coming from journals without crossing community boundaries (dark blue) versus external flow that does cross community boundaries (light blue) and (3) return flow after two steps on the network (dark red) versus lost flow after two steps on the network (light red). M1 is always the top bar and M2 is the bottom bar (see legend insert). The error bars indicate the 10th and 90th bootstrap percentiles. The error bars at the intersection of the stacked bars represent the variation in the quality, internal and return flows, respectively. The error bars at the end of the stacked bars represent the total variation in flow. M1 bars for quality and return flows do not show error bars, as the networks are exactly the same. The journals selected for this figure were chosen because they are mentioned in the primary text. (b) Largest gainers and losers in the top 100 journals when including effects of second-order Markov dynamics. The upper portion shows the journals that gain the most in flow and the lower portion shows the journals that lose the most in flow. Dark blue indicates a gain/loss in flow coming from journals without crossing community boundaries (internal flow). The light blue indicates a gain/loss in the flow that does cross community boundaries (external flow). The dark red shows the net gain and orange shows the net loss for each journal listed. The error bars indicate 10th and 90th bootstrap percentiles.
In contrast, the large multidisciplinary journals receive less flow from other top journals. In a first-order Markov model, they leak flow between communities and boost each other. For example, Science in a first-order Markov model receives flow from and then redistributes flow to journals in multiple fields, even if no readers would cross those field boundaries. In contrast, Science in a second-order Markov model mainly receives flow from and redistributes flow to journals within the same fields. As a significant fraction of the flow that leaks between fields in a first-order Markov model reaches multidisciplinary journals, they receive less flow in a second- relative to a first-order Markov model. As Fig. 4b illustrates, journals that increase from a first- to a second-order Markov model almost always see an increase in the flow from their primary community (internal flow). In general, journals that do not depend on leaking flow between modules gain flow, and journals that do, including multidisciplinary journals, lose flow, when two-step memory is taken into account.
We now turn to discussing the advantages of using a second-order Markov model for ranking journals. As we analyse rankings designed to capture dynamics, the issue with leaking flow of a first-order Markov model directly provides a reason for preferring a second-order Markov model. However, leaking flow is also indirectly associated with another important reason for preferring a second-order Markov model. All rankings are subject to gaming, and a good ranking ought to be difficult to manipulate. For example, the journal impact factor50, which simply counts the number of citations a journal receives in a given period of time, and corresponds to a zero-order Markov model, can easily be manipulated by editorial policies that encourage self-citations51.
A first-order Markov model, in particular one that ignores self-citations49, is more difficult to exploit, because the value of a citation depends on the ranking of the citing journal. As important journals need to be cited by important journals, insignificant journals cannot directly boost their own ranking. However, leaking flow is a weak point of this first-order ranking. For example, Fig. 1c illustrates that the first-order citation flows mix and leak from the ecology journals to the molecular biology journals through multidisciplinary PNAS. In this way, citations from ecology journals to multidisciplinary journals will indirectly boost molecular biology journals. For improving the ranking of the citing journal, leaking flow therefore creates a potential incentive to reduce the number of citations to multidisciplinary journals. This citation bias works against the principle that citations should go to the best work, and can have a negative influence on the quality of the ranking.
The problem caused by leaking flow is minor for a second-order ranking, as citation flows to multidisciplinary journals tend to return and stay within the citing field. This effect not only explains why multidisciplinary journals lose and field-specific journals gain when going from a first- to a second-order model as shown in Fig. 4b, it also reduces the influence on ranking caused by strategically excluding citations to multidisciplinary journals. For example, although the ranking of Ecology improves by removing citations to Science and PNAS, both with a first- and a second-order model, the effect is three times smaller with the second-order model. That is, a second-order Markov model for ranking journals is more robust to manipulation.
Memory and spreading processes
Previous work has considered temporal and memory effects on spreading by modelling time-respecting paths in temporal networks of contacts22,23,52 and bidirectional paths in mobility networks of commuters27,28,53,54. Our objective is to quantify the full effect of second-order Markov dynamics in general mobility patterns. Therefore, here we model spreading by considering unrestricted second-order Markov processes obtained from empirical pathways.
We considered two classical models for spreading processes9: a meta-population model that we implemented for the cities and is related to disease spreading, and a simpler model for spreading of ideas or rumours that we studied on the email data set. Both models are stochastic compartmental models. In the meta-population model we use SIR dynamics, and in the simpler model we use SI dynamics. S, I and R refer to different categories of individuals: susceptible individuals (S) are healthy individuals who have not been touched by the infection; infected individuals (I) have been reached by the epidemic and in turn can transmit the infection to other individuals; and recovered individuals (R) are those who reach immunization after being infected and cannot spread the disease anymore.
In the meta-population model, we observe that using a second-order Markov process has a negligible effect on the size of the epidemic, also known as the attack rate, and that it only slightly tends to slow down the spreading process. In contrast, in the simpler model we observe that second-order Markov dynamics significantly slow down the spreading process. We conclude that we only observe significant memory effects on the spreading dynamics when the path dependence is preserved at transmission. For the cities data set the effect of second-order Markov dynamics is negligible, because memory is lost at transmission between random individuals in cities and also because travellers do not return at sufficiently high rate compared with pure commuting traffic27,28,29,53 to limit the number of disease introductions in cities55. Below we provide a more detailed discussion.
First we consider modelling spreading with SIR dynamics and meta-populations for the cities data set. The model works in two steps, similar to the reaction–diffusion model proposed in ref. 56. During the reaction step, each infected individual can recover with probability μ and each susceptible individual can get infected by any infected individual in the same physical node. Effectively, the infection is transmitted regardless of where individuals were one step before and, therefore, describes full mixing at the physical node level. Let us define the total number of individuals in physical node i, Pi, and the total number of infected individuals in node i, Ii. We estimated the number of individuals in each city from the number of tickets in our data set that end in the cities and considered a total population of 300 million, which is a rough estimate of the total population of the United States. Assuming that the transmission rate is β/Pi, where β is a parameter that accounts for the virulence of the disease, the probability of each susceptible individual becoming infected is  . The transmission rate is the virulence factor divided by the total population of node i, because we assume that each individual can get in touch with a fixed number of other individuals56.
. The transmission rate is the virulence factor divided by the total population of node i, because we assume that each individual can get in touch with a fixed number of other individuals56.
After the reaction step, we carry out the diffusion of people in the city network with or without memory of their previous step. Each individual can move to neighbouring cities with probability σ if she is ready to start a new trip in a self-memory node, indicating that she was in the same physical node in the previous step, and with probability 1/τ if she is travelling and not in a self-memory node, indicating that she was not in the same physical node in the previous step. We use two different probabilities because the fraction of people who start a new trip from a self-memory node (from home) is much smaller than those who continue the trip after it started. We consider σ=10−3 per day, which is of the order of magnitude of the number of new itineraries per day divided by the total population (we estimate σ≃2 × 10−3 itineraries per person per day, from our data). The length of stay τ can be extremely short if a city is visited just to take a connecting flight. Although the length of stay is heterogeneously distributed53, we simply considered an average length of stay of 2 days. That is, once a trip started, each individual has a 50% chance of spending another day in the city she is visiting or of moving to the next city. From most memory nodes, it is possible to reach a self-memory node and end the trip, such that the probability of leaving again is σ.
After starting a trip, movements can be carried out with a first- or second-order Markov process. Starting from Anchorage and Los Angeles, Fig. 5a shows the difference in the evolution of the spreading process. We used μ−1=3 days, and two different values for the basic reproduction number R0=βμ−1=1.3 and 2, which is the average number of new infections caused by each infected individual before recovering. The total fraction of infected people at the end of the epidemic is barely affected (the difference is smaller than 10−4) and there is only a small delay in the spreading process. To estimate this delay, we measured the peak time, that is, the day in which the number of infected individuals is the highest. We averaged the peak times across different runs, with the 100 infected individuals in a particular city selected proportional to its population. For R0=1.3, we estimated the peak time with first-order memory dynamics to 160±8 and with second-order memory dynamics to 166±9. For R0=2, we estimated the peak time first-order memory dynamics to 62±3 and with second-order memory dynamics to 64±3. In both cases, the difference is ≃3%.
(a) Fraction of infected individuals (prevalence) as a function of time measured in days from the beginning of the process. The two curves represent a first- (M1) and a second-order (M2) Markov process. We seeded the outbreak with 100 infected individuals in Anchorage (top) and Los Angeles (bottom). (b) Prevalence as a function of time in a modified data set where people only travel to a city and come back. (c) Fraction of individuals that have received the rumour as a function of scaled time from the beginning of the process. The three curves show different level of mixing between the first- and second-order Markov model. The shaded area gives the 25 and 75 percentiles, and the solid curve is the median.
To better understand these results, we repeated the analysis after first removing all but short returning itineraries, such as New York–Chicago–New York. In this way, we can compare with the work on commuting traffic that has reported a slow down in the spreading process27,28,29,53. For these dynamics, although we still do not observe an effect on the attack rate, Fig. 5b shows that we observe a significant effect on the peak time by modelling commuting traffic with a second-order Markov process. With only commuting traffic, a second-order Markov model captures that travellers spend only limited amount in other cities, thereby reducing the effective connectivity and the number of disease introductions in cities. In the actual data, however, the number of one-way tickets and connecting flights is sufficiently large to reduce the return rate and increase the time spent in other cities to a level at which the effect on spreading vanishes between first- and second-order dynamics55. Again, once random transmission occurs in a city, all memory effects are washed out in this meta-population model. Therefore, the effect of a higher-order Markov process is primarily influential in the beginning of the outbreak during the introduction phase when the sequence of contacts matters22,23,52. Overall, we conclude that the first- and second-order dynamics must be sufficiently different to show a clear difference on the spreading. To quantify precisely how different is an interesting question for further investigation.
Secondly we consider modelling spreading with SI dynamics without meta-populations for the emails data set. In the email data set, each physical node represents an individual with a memory node for each other individual from which an email was received. The target of a memory node’s out-link represents the individual to which the email was forwarded to and the weight represents the total number of such emails that has been forwarded. We model emails as ‘hosts’ for rumours and each individual j can become infected (informed) if she receives an ‘infective’ email from an individual i. When this happens, memory node  associated with the source becomes infected and the individual is now informed. The infective email can be forwarded to another person k, according to the probability distribution
associated with the source becomes infected and the individual is now informed. The infective email can be forwarded to another person k, according to the probability distribution  . In this way, we model the spread of rumours as a simple contagion process without ‘stiflers’ who no longer spread rumours34. Therefore, we focus on the early stages of a spreading process. To study the robustness of the effects of this second-order Markov process, we also allow information to be spread independently of the source at different level of mixing between the first- and second-order Markov model. See Methods for details about the model.
. In this way, we model the spread of rumours as a simple contagion process without ‘stiflers’ who no longer spread rumours34. Therefore, we focus on the early stages of a spreading process. To study the robustness of the effects of this second-order Markov process, we also allow information to be spread independently of the source at different level of mixing between the first- and second-order Markov model. See Methods for details about the model.
For this model, we measured the speed of the spreading process. Figure 5c shows the average fraction of individuals that has heard about the rumour as a function of time, starting from a single infected memory node at time t=0. The initial nodes were randomly selected among those belonging to the largest strongly connected component. We scaled the time by multiplying by the rumour-spreading rate to make results independent of this parameter. Overall, the spreading is much slower when emails are modelled by a Markov model of second order, as this model can capture that most emails are forwarded within strongly confined modules of individuals, which also prevent them from reaching highly connected and efficient spreaders. Moreover, the main difference compared with the meta-population model is that an individual informed about a rumour can participate in multiple email conversations simultaneously without an interest in informing everybody about the rumour. That is, where information spreads often depends on from where it is coming.
Discussion
We have shown that a second-order Markov model is required to capture essential dynamical processes in a variety of integrated systems, with important consequences for community detection, ranking and information spreading. Recent work has indicated that a first-order Markov model may fail to adequately predict real dynamics15,20,23,26. That is, real dynamics often have at least one-step memory, which conventional network analysis cannot capture. To bridge this gap, we generalized three commonly used methods of community detection, ranking and spreading, to operate on a second-order Markov model of flow. We used several real-world and synthetic examples to show that these methods reveal system organizations that better correspond to actual structures, including increased return flow that confines flow in smaller and more overlapping modules. Previously, researchers have tried to reveal such structures with heuristic algorithms, but our approach uses more data rather than extra assumptions, and benchmark and bootstrap analyses show that these results are real and based on sufficient data. Consequently, we have demonstrated that using a second-order Markov model is often essential for fundamental methods in network science.
The combination of our examples indicates that memory is critical for analysing network flows in general, and we expect researchers throughout the sciences to find the methods useful for analysing increasingly available pathway data. Therefore, we have made data and code available online at http://www.icelab.org.umu.se/memorynetworks and integrated the community-detection algorithm in the Infomap sofware package available at http://www.mapequation.org. Our methods can be directly generalized to higher-order Markov models as well. Even if our statistical analysis of higher-order Markov models suggests that we have captured most of the salient features in the analysed systems, other systems where longer pathway data are relevant and available may have discernible higher-order features. We expect such features to be less salient, and other means of balancing model complexity and utility may be more appropriate.
Methods
Assembling pathways into networks with and without memory
Figure 6 illustrates how we generated the networks that describe the dynamics in Fig. 1a,b: from pathways in a, via weighted links in b and c, to directed weighted networks in d and e. First, we collect long pathways, in this example, of real itineraries from The Research and Innovative Technology Administration (Fig. 6a). The data contain each stop on 19 415 369 itineraries with average pathlength 3.3 between 464 airports in the United States. We used data from the first three quarters of 2011, which contain a sample of 10% of all itineraries during the time period. In the cities data set, we aggregated all airports within a radius of 50 km and called destinations by corresponding city names. Each pathway has a weight equal to the number of passengers who have purchased exactly that itinerary. To generate weighted directed links for the standard network, we counted bigrams (city pairs) in the itineraries (Fig. 6b). To generate weighted directed links for the memory network, we counted trigrams (city triplets) in the itineraries (Fig. 6c). In the airport data set, we focused on transfer traffic and disregarded one-way trips with a single flight (21% of all itineraries). In the cities data set, however, we focused on real passenger traffic for accurate modelling of disease spread and included also short pathways. Therefore, in the cities data set the typical memory averaged over all travellers is somewhat less than second order. Next, we assembled the links into networks. All links with the same start node in the bigrams represent out-links of the start node in the standard network (Fig. 6d). A physical node in the memory network, which corresponds to a regular node in a standard network, has one memory node for each in-link (Fig. 6e). A memory node represents a pair of nodes in the trigrams. For example, the blue memory node in Fig. 6e represents passengers who come to Chicago from New York. All links with the same start memory node in the trigrams represent out-links of the start memory node in the memory network. In this way, the memory network can maintain dependency between where passengers come from and where they go next. Figure 1a,b show the dramatic effect of maintaining second-order memory: passenger travel is much more constrained than what the standard network can capture. See Supplementary Note 1 for details of how we obtained pathways for all analysed networks and represented them as networks with and without memory.
(a) Itineraries weighted by passenger number. (b) Aggregated bigrams for links between physical nodes. (c) Aggregated trigrams for links between memory nodes. (d) Network without memory. (e) Network with memory. Corresponding dynamics in Fig. 1a,b.
Significance analysis with resampling
We performed two different statistical tests to validate our results, bootstrap resampling of all summary statistics in Table 1 and surrogate data testing of the Markov order in Fig. 2 and Supplementary Fig. 3. Bootstraping allows us to assign confidence intervals to the summary statistics based on resampling of the observed data set. Accordingly, only trigrams observed in the data will occur, but possibly with different frequencies. Contrarily, surrogate data testing allows us to also generate unobserved trigrams and is therefore suitable for hypothesis testing of the Markov order against a null model. In turn, we describe the two methods below.
For the bootstrapping, we generated 100 bootstrap replicas for each data set by resampling the weights of the pathways from a multinomial distribution (for patients, taxis and emails, we only had access to trigrams and resampled their weights directly). This scheme corresponds to resampling of all pathways with replacement. That is, we assume that pathways are generated independently. For the air traffic depicted in Fig. 6a, for example, we assume that tickets are bought independently. This assumption of independence is, of course, only approximately true, but as flight tickets rarely are bought for more than a few passengers at the same time, the approximation will work well in practice. After resampling the pathways, we generated the networks as described in Fig. 6b–e and performed any analysis as on the raw network. For each set of summary statistics, we calculated the bootstrap confidence interval by ordering the 100 bootstrap estimates and eliminated the ten smallest and ten largest estimates. In general, we report the lower and upper limits of this interval.
For the surrogate data testing, our null hypothesis was that the flow is first-order Markov, and we used the conditional entropy at each node as a test statistic. Assuming that the null hypothesis is true, we estimated the probability that the conditional entropy in a second-order Markov process is at least as low as the observed value. We estimated this probability, the P-value, with surrogate resampling and rejected the null hypothesis if the P-value was lower than 0.10. For each node and for each resampling, we removed the second-order Markov effect by performing random pairings between all nodes visited before and after the node given by all trigrams centred at the node. With this resampling scheme, we can single out nodes with a significant second-order Markov effect. See Supplementary Note 2, for further details and for surrogate testing of higher Markov orders.
Community detection with second-order Markov dynamics
We have chosen to work with the flow-based map equation framework30. In principle, we could have used alternative flow-based methods31, but the map equation framework allows us to compare the community structure with first- and second-order Markov dynamics by only modifying the dynamics and not the mechanics of the method. As we are interested in overlapping modules, we build our new method on a generalization of the map equation to overlapping modules39.
The map equation framework is an information-theoretic approach that takes advantage of the duality between compressing data and finding regularities in the data. Given module assignments of all nodes in the network, the map equation measures the description length of a random walker that moves from node to node by following the links between the nodes. Therefore, finding the optimal partition or cover of the network corresponds to testing different node assignments and picking the one that minimizes the description length30.
The map equation framework easily generalizes to higher-order Markov dynamics, because memory networks only change the dynamics of the random walker as described above. Therefore, instead of applying the search algorithm on the standard network, we apply it on the memory network and assign memory nodes to modules, with one important difference: as we are interested in movements with or without memory between physical nodes, the description of the random walker must reflect this process. Therefore, when two or more memory nodes of the same physical node are assigned to the same module, the description length must capture the fact that the memory nodes share the same codeword. We achieve this description by summing the visit frequencies of all memory nodes of each physical node in a module and then use this visit frequency to derive the optimal codeword length. We ensure that the community detection results only depend on memory effects by representing first-order Markov dynamics in a memory network, with each memory node having the out-links of its corresponding physical node in the standard network. In this way, the compression algorithm remains the same and only the dynamics change.
Figure 7 illustrates the effect of second-order Markov dynamics on community detection. The pathways represent air travel between San Francisco, Las Vegas and New York, and correspond to a subset of the itineraries in the city data. With first-order Markov dynamics, there are no regularities to take advantage of in a modular description, and clustering all the cities together gives a shorter description length. With second-order Markov dynamics, however, the strong out-and-back travel pattern to and from Las Vegas makes it more efficient to describe the dynamics as two overlapping modules, with Las Vegas assigned to both modules. That is, the first-order dynamics obscure the actual travel pattern and prevent a modular description from compressing the data. See Supplementary Note 3, for further details.
Pathway data between San Francisco, Las Vegas and New York, represented with memory nodes capturing first-order (a,b) and second-order (c,d) memory dynamics. With first-order memory, the characteristic out-and-back travel of Las Vegas is lost and the dynamics are best described as movements in one module; describing the dynamics with two overlapping modules requires 0.63 more bits. With second-order memory, the out-and-back travel is evident and the dynamics are best described as movements in two overlapping modules, as movements between the modules are very rare. See Supplementary Fig. 4 for a detailed derivation of the description lengths.
To validate our method, we have performed benchmark tests on synthetic pathways. We first describe how we build artificial pathways such that flow tends to stay inside predefined communities when described by a second-order Markov model. Next, we show that Infomap for memory networks, the community-detection algorithm we have developed, can recover the planted structure. However, when the artificial pathways are described by a first-order Markov model in a standard network, much of the structure is washed out. We show that neither Infomap nor other commonly used methods for overlapping communities can accurately recover the planted structure.
We used the following algorithm to generate trigrams within and between communities.
As planted structure, we consider 128 nodes and the community size fixed to 32 nodes, similar to that in the Girvan–Newman benchmark57. Moreover, we tune the number of communities M. If M=4, each node is assigned to a single community. If M>4, multiple memberships are assigned to nodes in random order, with the constraint that no node can be assigned to the same community twice.
As synthetic pathways, we draw Ein internal trigrams and Eout external trigrams. Internal trigrams are paths of three nodes i,j,k such that if nodes i and j belong to community C, node k also belongs to C. For external trigrams, at least two of the three nodes are not assigned to the same community. Below we describe a simple sampling algorithm. In these tests, we set Ein=50,000 and Eout=5,000 and 20,000, respectively. The number of trigrams is relatively high compared with the network size, because to highlight the effect of memory the number of trigrams must be of the same order of magnitude as the number of memory nodes (128 × 127≃15,000).
Internal trigrams confine flow inside communities. Therefore, if the flow goes from node i to j in community C, the next node k must also belong to community C. This constraint requires that memory nodes  and
and  are uniquely assigned to community C, although physical nodes i, j and k can have multiple memberships. We assign memberships to memory nodes and draw internal trigrams in the following way:
are uniquely assigned to community C, although physical nodes i, j and k can have multiple memberships. We assign memberships to memory nodes and draw internal trigrams in the following way:
-
We uniformly select a community C.
-
We uniformly sample nodes i, j and k assigned to community C. As nodes can be drawn from multiple clusters, we check that neither memory node
 nor memory node
nor memory node  has been assigned to a community different from C yet. If at least one has been assigned to a different cluster, we sample new nodes. If not, we assign the memory nodes to C and record the trigram i,j,k.
has been assigned to a community different from C yet. If at least one has been assigned to a different cluster, we sample new nodes. If not, we assign the memory nodes to C and record the trigram i,j,k.
External trigrams guide flow between communities. Therefore, we draw random trigrams i,j,k until at least two of the three nodes have no memberships in common.
To measure how well Infomap for memory networks recovers the planted structure, we applied the Normalized Mutual Information (NMI) described in ref. 58 to the community assignments of the memory nodes (we used max function for the normalization instead of the average). Some memory nodes were only sampled in external trigrams and not assigned a membership by the algorithm above. As these nodes are not present in the planted structure, we also discard them in the output of Infomap. Figure 8 show the performance of Infomap for memory networks with first- and second-order Markov dynamics, as well as the performance of standard (undirected) Infomap30 with all memory nodes treated as physical nodes. Infomap for memory networks recovers the planted partitions almost perfectly up to at least 8 community assignments per node with 5,000 external trigrams and up to 6 community assignments per node with 20,000 external trigrams. However, with first-order dynamics, Infomap for memory networks is only able to recover the correct partition when no overlap is present. Quite the opposite, standard Infomap tends to find many more modules because the algorithm considers each memory node to be ‘independent,’ and there is no intrinsic compression gain from clustering memory nodes of the same physical node together.
Performance of Infomap. The blue and red curves refer to M1 and M2 structural information, respectively, whereas the yellow curve was obtained by running standard (undirected) Infomap on a network in which each memory node is treated as a physical node. Lines show median values and shaded areas cover 25 and 75 percentiles.
To demonstrate that second-order Markov information is necessary, we aggregated the trigrams into standard undirected networks and applied several commonly used algorithms for overlapping communities. As the nodes can be assigned to multiple communities, we used the definition of NMI proposed in ref. 59 for all methods except for the link-clustering method. This algorithm returns a partition of non-overlapping links, which we treated as memory nodes and computed the NMI as described for Infomap above. As the link clustering method only accepts unweighted graphs as input, we used a threshold of 12 for link weights and 0.7 for selecting a partition from the dendrogram, and found that results are not sensitive to these choices. Further, the clique percolation method was unusably slow with all links included and we had to remove links with weights below a certain threshold. We used a threshold of 3 for 5,000 external trigrams and 8 for 20,000 external trigrams. We also had to provide the clique size (≃30).
Table 2 shows the results. The clique percolation method was the only algorithm that was able to recover the correct partition with external trigrams and multiple community assignments. However, regardless of the thresholds we tried, for more than two community assignments per node we were not able to obtain any result after several days of running time. The reason why the algorithm is successful on this benchmark test, at least in theory, is that the number of trigrams is so high that the planted communities are cliques of 32 nodes. Of all tested algorithms, the link clustering method was the only one that obtained non-trivial solutions for three or more community assignments per node. In the next section, we illustrate how clique percolation and link clustering can identify overlapping communities of second-order dynamics aggregated in standard networks.
Ergodic second-order Markov dynamics
The solution of equation (10) is not well-defined when the process is not ergodic, which happens when the memory network is not strongly connected, or when it contains closed cycles60. To circumvent this limitation and to ensure the ergodicity of the stochastic process, we perform two modifications. First, if a memory node is a dangling node and has no out-links, we use M1 data and assign all out-links from the physical node to the dangling node. In this way, link weights and M1 data become our fallbacks when there is not enough M2 data for an ergodic process on the memory network. Second, it is standard to allow walkers to randomly teleport across the system, as we mentioned before. Walkers either follow links with probability α or teleport with probability 1−α (ref. 6). Therefore, the PageRank of a memory node is given by

It is important to note that walkers do not teleport uniformly to memory nodes, but at a rate proportional to the weight W of the corresponding link. Equivalently, walkers thus teleport to physical nodes at a rate proportional to their in-strength. This choice is motivated by recent research showing that so-called link teleportation improves robustness of ranking with respect to standard teleportation61. A random walk with teleportation is ergodic for any α<1, whatever the topology of the underlying network, and its stationary solution can be found by using standard iteration methods.
The link-teleportation scheme works well for ranking nodes, but further improvements can be made for the map equation, which also explicitly operates on the flow between nodes. For community-detection results that are more robust to the particular choice of teleportation parameter, we do not use teleportation steps between nodes and only steps along links to derive the optimal codeword lengths. We achieve the same PageRank of memory nodes in equation (12) by first calculating the stationary distribution with recorded teleportation to physical nodes at a rate proportional to their out-strength, followed by a subsequent recorded step without teleportation. By only encoding the last step in this smart teleportation scheme61, the community detection results are based on the same ergodic node visit rates as in equation (12), but without the noise on links caused by random teleportation.
SI dynamics on networks with memory
Here we describe how we model spreading with SI dynamics without meta-populations for the emails data set. We assume that each memory node  forwards
forwards  emails per time step, where φ is a proportionality constant and
emails per time step, where φ is a proportionality constant and  is the out-strength of the memory node, that is, the sum of the weights of the links
is the out-strength of the memory node, that is, the sum of the weights of the links  . A forwarded email from memory node
. A forwarded email from memory node  goes to a memory node, say
goes to a memory node, say  , with probability
, with probability  . If
. If  is informed about a rumour and
is informed about a rumour and  is not, we assume that an email from
is not, we assume that an email from  with probability β, the so-called rumour spreading rate. Let
with probability β, the so-called rumour spreading rate. Let  denote the overall probability that an infected memory node
denote the overall probability that an infected memory node  transmits the rumour to an uninformed memory node
transmits the rumour to an uninformed memory node  . As the probability that the infection is not transmitted is the probability that each email leaving
. As the probability that the infection is not transmitted is the probability that each email leaving  either is forwarded to a memory node other than
either is forwarded to a memory node other than  or is forwarded to
or is forwarded to  but ignored, we have:
but ignored, we have:

where we assume that β is small and  is simply the weight of link
is simply the weight of link  in the memory network. In this limit, the only relevant parameter is thus βφ. Without loss of generality, we can set φ=1, in which case the dynamics of the spreading process are driven by
in the memory network. In this limit, the only relevant parameter is thus βφ. Without loss of generality, we can set φ=1, in which case the dynamics of the spreading process are driven by

This equation shows that this spreading process with second-order Markov dynamics corresponds to traditional spreading models but performed on memory nodes. That is, the only differences are that emails are forwarded to the next destination depending on where they come from. As rumours not necessarily need to spread between individuals that participate in the same email conversations, we allow each informed individual to send emails according to a first-order Markov model with probability η at each time step. Therefore, to study the effects of memory on this spreading process, we can simply tune η. For example, the extreme case η=100% corresponds to a first-order Markov model.
Additional information
How to cite this article: Rosvall, M. et al. Memory in network flows and its effects on spreading dynamics and community detection. Nat. Commun. 5:4630 doi: 10.1038/ncomms5630 (2014).
References
Watts, D. & Strogatz, S. Collective dynamics of ‘small-world’ networks. Nature 393, 440–442 (1998).
Barabási, A. & Albert, R. Emergence of scaling in random networks. Science 286, 509–512 (1999).
Barrat, A., Barthelemy, M., Pastor-Satorras, R. & Vespignani, A. The architecture of complex weighted networks. Proc. Natl Acad. Sci. USA 101, 3747 (2004).
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M. & Hwang, D. Complex networks: structure and dynamics. Phys. Rep. 424, 175–308 (2006).
Granovetter, M. The strength of weak ties: a network theory revisited. Sociol. Theory 1, 201–233 (1983).
Brin, S. & Page, L. The anatomy of a large-scale hypertextual web search engine. Comput. Networks ISDN 30, 107–117 (1998).
Brockmann, D., Hufnagel, L. & Geisel, T. The scaling laws of human travel. Nature 439, 462–465 (2006).
Balcan, D. et al. Multiscale mobility networks and the spatial spreading of infectious diseases. Proc. Natl Acad. Sci. USA 106, 21484–21489 (2009).
Vespignani, A. Modelling dynamical processes in complex socio-technical systems. Nat. Phys. 8, 32–39 (2012).
Shannon, C. E. A mathematical theory of communication. Bell Syst. Tech. J. 27, 379–423 (1948).
Box, G. E., Jenkins, G. M. & Reinsel, G. C. Time Series Analysis: Forecasting and Control John Wiley & Sons (2013).
Kareiva, P. & Shigesada, N. Analyzing insect movement as a correlated random walk. Oecologia 56, 234–238 (1983).
Robins, G., Snijders, T., Wang, P., Handcock, M. & Pattison, P. Recent developments in exponential random graph (p*) models for social networks. Soc. Networks 29, 192–215 (2007).
Meiss, M. R., Menczer, F., Fortunato, S., Flammini, A. & Vespignani, A. inProc. Internat. Conf. on Web Search and Web Data Mining 65–76ACM (2008).
Chierichetti, F., Kumar, R., Raghavan, P. & Sarlós, T. inProc. 21st Internat. Conf. on World Wide Web 609–618ACM (2012).
Asztalos, A. & Toroczkai, Z. Network discovery by generalized random walks. Europhys. Lett. 92, 50008 (2010).
Backstrom, L. & Leskovec, J. inProc. fourth ACM Internat. Conf. on Web Search and Data Mining 635–644ACM (2011).
Singer, P., Helic, D., Taraghi, B. & Strohmaier, M. Memory and structure in human navigation patterns. Preprint at http://arXiv.org/abs/1402.0790 (2014).
Iribarren, J. L. & Moro, E. Impact of human activity patterns on the dynamics of information diffusion. Phys. Rev. Lett. 103, 038702 (2009).
Takaguchi, T., Nakamura, M., Sato, N., Yano, K. & Masuda, N. Predictability of conversation partners. Phys. Rev. X 1, 011008 (2011).
Holme, P. & Saramäki, J. Temporal networks. Phys. Rep. 519, 97–125 (2012).
Lentz, H. H., Selhorst, T. & Sokolov, I. M. Unfolding accessibility provides a macroscopic approach to temporal networks. Phys. Rev. Lett. 110, 118701 (2013).
Pfitzner, R., Scholtes, I., Garas, A., Tessone, C. J. & Schweitzer, F. Betweenness preference: quantifying correlations in the topological dynamics of temporal networks. Phys. Rev. Lett. 110, 198701 (2013).
Gonzalez, M., Hidalgo, C. & Barabási, A. Understanding individual human mobility patterns. Nature 453, 779–782 (2008).
Heath, M., Vernon, M. & Webb, C. Construction of networks with intrinsic temporal structure from UK cattle movement data. BMC Vet. Res. 4, 11 (2008).
Song, C., Qu, Z., Blumm, N. & Barabási, A. Limits of predictability in human mobility. Science 327, 1018–1021 (2010).
Balcan, D. & Vespignani, A. Phase transitions in contagion processes mediated by recurrent mobility patterns. Nat. Phys. 7, 581–586 (2011).
Belik, V., Geisel, T. & Brockmann, D. Natural human mobility patterns and spatial spread of infectious diseases. Phys. Rev. X 1, 011001 (2011).
Poletto, C., Tizzoni, M. & Colizza, V. Human mobility and time spent at destination: Impact on spatial epidemic spreading. J. Theor. Biol. 338, 41–58 (2013).
Rosvall, M. & Bergstrom, C. Maps of random walks on complex networks reveal community structure. Proc. Natl Acad. Sci. USA 105, 1118 (2008).
Delvenne, J., Yaliraki, S. & Barahona, M. Stability of graph communities across time scales. Proc. Natl Acad. Sci. USA 107, 12755–12760 (2010).
May, R. & Lloyd, A. Infection dynamics on scale-free networks. Phys. Rev. E 64, 066112 (2001).
Pastor-Satorras, R. & Vespignani, A. Epidemic spreading in scale-free networks. Phys. Rev. Lett. 86, 3200–3203 (2001).
Nekovee, M., Moreno, Y., Bianconi, G. & Marsili, M. Theory of rumour spreading in complex social networks. Phys. A 374, 457–470 (2007).
Bergstrom, C., West, J. & Wiseman, M. The eigenfactor metrics. J. Neurosci. 28, 11433–11434 (2008).
Parry, W. Intrinsic markov chains. Trans. Am. Math. Soc. 112, 55–66 (1964).
Sinatra, R., Gómez-Gardeñes, J., Lambiotte, R., Nicosia, V. & Latora, V. Maximal-entropy random walks in complex networks with limited information. Phys. Rev. E 83, 030103 (2011).
Van der Heyden, M., Diks, C., Hoekstra, B. & DeGoede, J. Testing the order of discrete Markov chains using surrogate data. Phys. D 117, 299–313 (1998).
Esquivel, A. & Rosvall, M. Compression of flow can reveal overlapping-module organization in networks. Phys. Rev. X 1, 021025 (2011).
Scholtes, I. et al. Slow-down vs. speed-up of information diffusion in non-markovian temporal networks. Preprint at http://arXiv.org/abs/1307.4030 (2013).
Lambiotte, R., Salnikov, V. & Rosvall, M. Effect of memory on the dynamics of random walks on networks. Preprint at http://arXiv.org/abs/1401.0447 (2014).
Newman, M. Modularity and community structure in networks. Proc. Natl Acad. Sci. USA 103, 8577–8582 (2006).
Lancichinetti, A., Radicchi, F., Ramasco, J. & Fortunato, S. Finding statistically significant communities in networks. PLoS ONE 6, e18961 (2011).
Ahn, Y., Bagrow, J. & Lehmann, S. Link communities reveal multiscale complexity in networks. Nature 466, 761–764 (2010).
Evans, T. & Lambiotte, R. Line graphs, link partitions, and overlapping communities. Phys. Rev. E 80, 016105 (2009).
Yang, J. & Leskovec, J. inProc. ACM SIGKDD Workshop on Mining Data Semantics 3, ACM (2012).
Palla, G., Derényi, I., Farkas, I. & Vicsek, T. Uncovering the overlapping community structure of complex networks in nature and society. Nature 435, 814–818 (2005).
Bohlin, L., Esquivel, A. V., Lancichinetti, A. & Rosvall, M. Robustness of journal rankings by network flows with different amounts of memory. Preprint at http://arXiv.org/abs/1405.7832 (2014).
West, J. D., Bergstrom, T. C. & Bergstrom, C. T. The Eigenfactor metrics: A network approach to assessing scholarly journals. Coll. Res. Libr. 71, 236–244 (2010).
Garfield, E. The history and meaning of the journal impact factor. JAMA 295, 90–93 (2006).
Monastersky, R. The number that’s devouring science. Chron. High. Educ. 52, A12 (2005).
Rocha, L. E., Liljeros, F. & Holme, P. Simulated epidemics in an empirical spatiotemporal network of 50,185 sexual contacts. PLoS Comput. Biol. 7, e1001109 (2011).
Poletto, C., Tizzoni, M. & Colizza, V. Heterogeneous length of stay of hosts' movements and spatial epidemic spread. Sci. Rep. 2, 476 (2012).
Keeling, M., Danon, L., Vernon, M. & House, T. Individual identity and movement networks for disease metapopulations. Proc. Natl Acad. Sci. USA 107, 8866–8870 (2010).
Lessler, J., Kaufman, J. H., Ford, D. A. & Douglas, J. V. The cost of simplifying air travel when modeling disease spread. PLoS ONE 4, e4403 (2009).
Colizza, V., Pastor-Satorras, R. & Vespignani, A. Reaction–diffusion processes and metapopulation models in heterogeneous networks. Nat. Phys. 3, 276–282 (2007).
Girvan, M. & Newman, M. E. Community structure in social and biological networks. Proc. Natl Acad. Sci. USA 99, 7821–7826 (2002).
Danon, L., Daz-Guilera, A., Duch, J. & Arenas, A. Comparing community structure identification. J. Stat. Mech. Theor. Exp. 2005, P09008 (2005).
Lancichinetti, A., Fortunato, S. & Kertész, J. Detecting the overlapping and hierarchical community structure in complex networks. New J. Phys. 11, 033015 (2009).
Langville, A. & Meyer, C. Deeper inside PageRank. Int. Math. 1, 335–380 (2004).
Lambiotte, R. & Rosvall, M. Ranking and clustering of nodes in networks with smart teleportation. Phys. Rev. E 85, 056107 (2012).
Gregory, S. Finding overlapping communities in networks by label propagation. New J. Phys. 12, 103018 (2010).
McDaid, A. & Hurley, N. in:Advances in Social Networks Analysis and Mining (ASONAM), 2010 International Conference 112–119IEEE (2010).
Acknowledgements
We thank F. Liljeros for extracting the patient data and JSTOR for providing the journal citation data. We also thank D. Edler, A. Eklöf, D. Kolp, C. Poletto and D. Vilhena for many discussions. M.R. was supported by the Swedish Research Council grant 2012-3729. R.L. was supported by the Belgian Network DYSCO, funded by the IAP Programme initiated by Belspo.
Author information
Authors and Affiliations
Contributions
M.R., A.V.E. and R.L. conceived the project. M.R. developed the community-detection algorithm. A.V.E. assembled the data and carried out the significance analysis. A.L. developed the epidemic and memory models. J.D.W. performed the ranking analysis. R.L. derived the analytical results. M.R. wrote the manuscript and all authors wrote the Supplementary Information. All authors were involved in interpreting the results and commented on the manuscript at all stages.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-9, Supplementary Tables 1-4, Supplementary Notes 1-4 and Supplementary References (PDF 772 kb)
Rights and permissions
About this article
Cite this article
Rosvall, M., Esquivel, A., Lancichinetti, A. et al. Memory in network flows and its effects on spreading dynamics and community detection. Nat Commun 5, 4630 (2014). https://doi.org/10.1038/ncomms5630
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms5630
This article is cited by
-
Multi-Linear Pseudo-PageRank for Hypergraph Partitioning
Journal of Scientific Computing (2024)
-
Single-trajectory map equation
Scientific Reports (2023)
-
Predicting variable-length paths in networked systems using multi-order generative models
Applied Network Science (2023)
-
Mapping change in higher-order networks with multilevel and overlapping communities
Applied Network Science (2023)
-
Locating community smells in software development processes using higher-order network centralities
Social Network Analysis and Mining (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.








 nor memory node
nor memory node  has been assigned to a community different from C yet. If at least one has been assigned to a different cluster, we sample new nodes. If not, we assign the memory nodes to C and record the trigram i,j,k.
has been assigned to a community different from C yet. If at least one has been assigned to a different cluster, we sample new nodes. If not, we assign the memory nodes to C and record the trigram i,j,k.