Abstract
Learning from data has led to paradigm shifts in a multitude of disciplines, including web, text and image search, speech recognition, as well as bioinformatics. Can machine learning enable similar breakthroughs in understanding quantum many-body systems? Here we develop an efficient deep learning approach that enables spatially and chemically resolved insights into quantum-mechanical observables of molecular systems. We unify concepts from many-body Hamiltonians with purpose-designed deep tensor neural networks, which leads to size-extensive and uniformly accurate (1 kcal mol−1) predictions in compositional and configurational chemical space for molecules of intermediate size. As an example of chemical relevance, the model reveals a classification of aromatic rings with respect to their stability. Further applications of our model for predicting atomic energies and local chemical potentials in molecules, reliable isomer energies, and molecules with peculiar electronic structure demonstrate the potential of machine learning for revealing insights into complex quantum-chemical systems.
Similar content being viewed by others
Introduction
Chemistry permeates all aspects of our life, from the development of new drugs to the food that we consume and materials we use on a daily basis. Chemists rely on empirical observations based on creative and painstaking experimentation that leads to eventual discoveries of molecules and materials with desired properties and mechanisms to synthesize them. Many discoveries in chemistry can be guided by searching large databases of experimental or computational molecular structures and properties by using concepts based on chemical similarity. Because the structure and properties of molecules are determined by the laws of quantum mechanics, ultimately chemical discovery must be based on fundamental quantum principles. Indeed, electronic structure calculations and intelligent data analysis (machine learning) have recently been combined aiming towards the goal of accelerated discovery of chemicals with desired properties1,2,3,4,5,6,7,8. However, so far the majority of these pioneering efforts have focused on the construction of reduced models trained on large data sets of density-functional theory calculations.
In this work, we develop an efficient deep learning approach that enables spatially and chemically resolved insights into quantum-mechanical properties of molecular systems beyond those trivially contained in the training dataset. Obviously, computational models are not predictive if they lack accuracy. In addition to being interpretable, size-extensive and efficient, our deep tensor neural network (DTNN) approach is uniformly accurate (1 kcal mol−1) throughout compositional and configurational chemical space. On the more fundamental side, the mathematical construction of the DTNN model provides statistically rigorous partitioning of extensive molecular properties into atomic contributions—a long-standing challenge for quantum-mechanical calculations of molecules.
Results
Molecular deep tensor neural networks
It is common to use a carefully chosen representation of the problem at hand as a basis for machine learning9,10,11. For example, molecules can be represented as Coulomb matrices7,12,13, scattering transforms14, bags of bonds15, smooth overlap of atomic positions16,17 or generalized symmetry functions18,19. Kernel-based learning of molecular properties transforms these representations non-linearly by virtue of kernel functions. In contrast, deep neural networks20 are able to infer the underlying regularities and learn an efficient representation in a layer-wise fashion21.
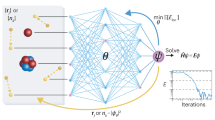
Molecular properties are governed by the laws of quantum mechanics, which yield the remarkable flexibility of chemical systems, but also impose constraints on the behaviour of bonding in molecules. The approach presented here utilizes the many-body Hamiltonian concept for the construction of the DTNN architecture (Fig. 1), embracing the principles of quantum chemistry, while maintaining the full flexibility of a complex data-driven learning machine.
(a) Molecules are encoded as input for the neural network by a vector of nuclear charges and an inter-atomic distance matrix. This description is complete and invariant to rotation and translation. (b) Illustration of the network architecture. Each atom type corresponds to a vector of coefficients  , which is repeatedly refined by interactions vij. The interactions depend on the current representation
, which is repeatedly refined by interactions vij. The interactions depend on the current representation  , as well as the distance Dij to an atom j. After T iterations, an energy contribution Ei is predicted for the final coefficient vector
, as well as the distance Dij to an atom j. After T iterations, an energy contribution Ei is predicted for the final coefficient vector  . The molecular energy E is the sum over these atomic contributions. (c) Mean absolute errors of predictions for the GDB-9 dataset of 133,885 molecules as a function of the number of atoms. The employed neural network uses two interaction passes (T=2) and 50,000 reference calculation during training. The inset shows the error of an equivalent network trained on 5,000 GDB-9 molecules with 20 or more atoms, as small molecules with 15 or less atoms are added to the training set. (d) Extract from the calculated (black) and predicted (orange) molecular dynamics trajectory of toluene. The curve on the right shows the agreement of the predicted and calculated energy distributions. (e) Energy contribution Eprobe (or local chemical potential
. The molecular energy E is the sum over these atomic contributions. (c) Mean absolute errors of predictions for the GDB-9 dataset of 133,885 molecules as a function of the number of atoms. The employed neural network uses two interaction passes (T=2) and 50,000 reference calculation during training. The inset shows the error of an equivalent network trained on 5,000 GDB-9 molecules with 20 or more atoms, as small molecules with 15 or less atoms are added to the training set. (d) Extract from the calculated (black) and predicted (orange) molecular dynamics trajectory of toluene. The curve on the right shows the agreement of the predicted and calculated energy distributions. (e) Energy contribution Eprobe (or local chemical potential  , see text) of a hydrogen test charge on a
, see text) of a hydrogen test charge on a  isosurface for various molecules from the GDB-9 dataset for a DTNN model with T=2.
isosurface for various molecules from the GDB-9 dataset for a DTNN model with T=2.
DTNN receives molecular structures through a vector of nuclear charges Z and a matrix of atomic distances D ensuring rotational and translational invariance by construction (Fig. 1a). The distances are expanded in a Gaussian basis, yielding a feature vector  , which accounts for the different nature of interactions at various distance regimes. Similar approaches have been applied to the entries of the Coulomb matrix for the prediction of molecular properties before12.
, which accounts for the different nature of interactions at various distance regimes. Similar approaches have been applied to the entries of the Coulomb matrix for the prediction of molecular properties before12.
The total energy EM for the molecule M composed of N atoms is written as a sum over N atomic energy contributions Ei, thus satisfying permutational invariance with respect to atom indexing. Each atom i is represented by a coefficient vector  , where B is the number of basis functions, or features. Motivated by quantum-chemical atomic basis set expansions, we assign an atom type-specific descriptor vector
, where B is the number of basis functions, or features. Motivated by quantum-chemical atomic basis set expansions, we assign an atom type-specific descriptor vector  to these coefficients
to these coefficients  . Subsequently, this atomic expansion is repeatedly refined by pairwise interactions with the surrounding atoms
. Subsequently, this atomic expansion is repeatedly refined by pairwise interactions with the surrounding atoms

where the interaction term vij reflects the influence of atom j at a distance Dij on atom i. Note that this refinement step is seamlessly integrated into the architecture of the molecular DTNN, and is therefore adapted throughout the learning process. In Supplementary Discussion, we show the relation to convolutional neural networks that have been applied to images, speech and text with great success because of their ability to capture local structure22,23,24,25,26,27. Considering a molecule as a graph, T refinements of the coefficient vectors are comprised of all walks of length T through the molecule ending at the corresponding atom28,29. From the point of view of many-body interatomic interactions, subsequent refinement steps t correlate atomic neighbourhoods with increasing complexity.
While the initial atomic representations only consider isolated atoms, the interaction terms characterize how the basis functions of two atoms overlap with each other at a certain distance. Each refinement step is supposed to reduce these overlaps, thereby embedding the atoms of the molecule into their chemical environment. Following this procedure, the DTNN implicitly learns an atom-centered basis that is unique and efficient with respect to the property to be predicted.
Non-linear coupling between the atomic vector features and the interatomic distances is achieved by a tensor layer30,31,32, such that the coefficient k of the refinement is given by

where bk is the bias of feature k and Wc and Wd are the weights of atom representation and distance, respectively. The slice Vk of the parameter tensor  combines the inputs multiplicatively. Since V incorporates many parameters, using this kind of layer is both computationally expensive as well as prone to overfitting. Therefore, we employ a low-rank tensor factorization, as described in (ref. 33), such that
combines the inputs multiplicatively. Since V incorporates many parameters, using this kind of layer is both computationally expensive as well as prone to overfitting. Therefore, we employ a low-rank tensor factorization, as described in (ref. 33), such that

where ‘’ represents element-wise multiplication, while Wcf,  , Wdf,
, Wdf,  and Wfc are the weight matrices and corresponding biases of atom representations, distances and resulting factors, respectively. As the dimensionality of Wcfcj and
and Wfc are the weight matrices and corresponding biases of atom representations, distances and resulting factors, respectively. As the dimensionality of Wcfcj and  corresponds to the number of factors, choosing only a few drastically decreases the number of parameters, thus solving both issues of the tensor layer at once.
corresponds to the number of factors, choosing only a few drastically decreases the number of parameters, thus solving both issues of the tensor layer at once.
Arriving at the final embedding after a given number of interaction refinements, two fully-connected layers predict an energy contribution from each atomic coefficient vector, such that their sum corresponds to the total molecular energy EM. Therefore, the DTNN architecture scales with the number of atoms in a molecule, fully capturing the extensive nature of the energy. All weights, biases, as well as the atom type-specific descriptors were initialized randomly and trained using stochastic gradient descent.
Learning molecular energies
To demonstrate the versatility of the proposed DTNN, we train models with up to three interaction passes T=3 for both compositional and configurational degrees of freedom in molecular systems. The DTNN accuracy saturates at T=3, and leads to a strong correlation between atoms in molecules, as can be visualized by the complexity of the potential learned by the network (Fig. 1e). For training, we employ chemically diverse data sets of equilibrium molecular structures, as well as molecular dynamics (MD) trajectories for small molecules. We employ two subsets of the GDB-13 database34,35 referred to as GDB-7, including >7,000 molecules with up to seven heavy (C, N, O, F) atoms, and GDB-9, consisting of 133,885 molecules with up to nine heavy atoms36. In both cases, the learning task is to predict the molecular total energy calculated with density-functional theory (DFT). All GDB molecules are stable and synthetically accessible according to organic chemistry rules35. Molecular features such as functional groups or signatures include single, double and triple bonds; (hetero-) cycles, carboxy, cyanide, amide, amine, alcohol, epoxy, sulphide, ether, ester, chloride, aliphatic and aromatic groups. For each of the many possible stoichiometries, many constitutional isomers are considered, each being represented only by a low-energy conformational isomer.
As Supplementary Table 1 demonstrates, DTNN achieves a mean absolute error of 1.0 kcal mol−1 on both GDB data sets, training on 5.8 k GDB-7 (80%) and 25 k (20%) GDB-9 reference calculations, respectively. Figure 1c shows the performance on GDB-9 depending on the size of the molecule. We observe that larger molecules have lower errors because of their abundance in the training data. However, when predicting larger molecules than present in the training set, the errors increase. This is because the molecules in the GDB-9 set are quite small, so we considered all atoms to be in each other’s chemical environment. Imposing a distance cutoff to interatomic interactions of 3 Å leads to a 0.1 kcal mol−1 increase in the error. However, this distance cutoff restricts only the direct interactions considered in the refinement steps. With multiple refinements, the effective cutoff increases by a factor of T because of indirect interactions over multiple atoms. Given large enough molecules, so that a reasonable distance cutoff can be chosen, scaling to larger molecules will require only to have well-represented local environments. For now, we observe that at least a few larger molecules are needed to achieve a good prediction accuracy. Following this train of thought, we trained the network on a restricted subset of 5 k molecules with >20 atoms. By adding smaller molecules to the training set, we are able to reduce the test error from 2.1 kcal mol−1 to <1.5 kcal mol−1 (see inset in Fig. 1c). This result demonstrates that our model is able to transfer knowledge learned from small molecules to larger molecules with diverse functional groups.
While only encompassing conformations of a single molecule, reproducing MD simulation trajectories poses a radically different challenge to predicting energies of purely equilibrium structures. We learned potential energies for MD trajectories of benzene, toluene, malonaldehyde and salicylic acid, carried out at a rather high temperature of 500 K to achieve exhaustive exploration of the potential-energy surface of such small molecules. The neural network yields mean absolute errors of 0.05, 0.18, 0.17 and 0.39 kcal mol−1 for these molecules, respectively (Supplementary Table 1). Figure 1d shows the excellent agreement between the DFT and DTNN MD trajectory of toluene, as well as the corresponding energy distributions. The DTNN errors are much smaller than the energy of thermal fluctuations at room temperature (∼0.6 kcal mol−1), meaning that DTNN potential-energy surfaces can be utilized to calculate accurate molecular thermodynamic properties by virtue of Monte Carlo simulations.
Supplementary Figs 1 and 2 illustrate how the performance of DTNN depends on the number of employed reference calculations and refinement steps (Supplementary Discussion). The ability of DTNN to accurately describe equilibrium structures within the GDB-9 database and MD trajectories of selected molecules of chemical relevance demonstrates the feasibility of developing a universal machine learning architecture that can capture compositional as well as configurational degrees of freedom in the vast chemical space. While the employed architecture of the DTNN is universal, the learned coefficients are different for GDB-9 and MD trajectories of single molecules.
Local chemical potential
Beyond predicting accurate energies, the true power of DTNN lies in its ability to provide novel quantum-chemical insights. In the context of DTNN, we define a local chemical potential  as an energy of a certain atom type A, located at a position r in the molecule M. While the DTNN models the interatomic interactions, we only allow the atoms of the molecule act on the probe atom, while the probe does not influence the molecule. The spatial and chemical sensitivity provided by our DTNN approach is shown in Fig. 1e for a variety of fundamental molecular building blocks. In this case, we employed hydrogen as a test charge, while the results for
as an energy of a certain atom type A, located at a position r in the molecule M. While the DTNN models the interatomic interactions, we only allow the atoms of the molecule act on the probe atom, while the probe does not influence the molecule. The spatial and chemical sensitivity provided by our DTNN approach is shown in Fig. 1e for a variety of fundamental molecular building blocks. In this case, we employed hydrogen as a test charge, while the results for  are shown in Fig. 2. Despite being trained only on total energies of molecules, the DTNN approach clearly grasps fundamental chemical concepts such as bond saturation and different degrees of aromaticity. For example, the DTNN model predicts the C6O3H6 molecule to be ‘more aromatic’ than benzene or toluene (Fig. 1e). Remarkably, it turns out that C6O3H6 does have higher ring stability than both benzene and toluene and DTNN predicts it to be the molecule with the most stable aromatic carbon ring among all molecules in the GDB-9 database (Fig. 3). Further chemical effects learned by the DTNN model are shown in Fig. 2 that demonstrates the differences in the chemical potential distribution of H, C, N and O atoms in benzene, toluene, salicylic acid and malonaldehyde. For example, the chemical potentials of different atoms over an aromatic ring are qualitatively different for H, C, N and O atoms—an evident fact for a trained chemist. However, the subtle chemical differences described by DTNN are accompanied by chemically accurate predictions—a challenging task for humans.
are shown in Fig. 2. Despite being trained only on total energies of molecules, the DTNN approach clearly grasps fundamental chemical concepts such as bond saturation and different degrees of aromaticity. For example, the DTNN model predicts the C6O3H6 molecule to be ‘more aromatic’ than benzene or toluene (Fig. 1e). Remarkably, it turns out that C6O3H6 does have higher ring stability than both benzene and toluene and DTNN predicts it to be the molecule with the most stable aromatic carbon ring among all molecules in the GDB-9 database (Fig. 3). Further chemical effects learned by the DTNN model are shown in Fig. 2 that demonstrates the differences in the chemical potential distribution of H, C, N and O atoms in benzene, toluene, salicylic acid and malonaldehyde. For example, the chemical potentials of different atoms over an aromatic ring are qualitatively different for H, C, N and O atoms—an evident fact for a trained chemist. However, the subtle chemical differences described by DTNN are accompanied by chemically accurate predictions—a challenging task for humans.
 for A={C, N, O, H} atoms.
for A={C, N, O, H} atoms.Because DTNN provides atomic energies by construction, it allows us to classify molecules by the stability of different building blocks, for example aromatic rings or methyl groups. An example of such classification is shown in Fig. 3, where we plot the molecules with most stable and least stable carbon aromatic rings in GDB-9. The distribution of atomic energies is shown in Supplementary Fig. 3, while Supplementary Fig. 4 lists the full stability ranking. The DTNN classification leads to interesting stability trends, notwithstanding the intrinsic non-uniqueness of atomic energy partitioning. However, unlike atomic projections employed in electronic-structure calculations, the DTNN approach has a firm foundation in statistical learning theory. In quantum-chemical calculations, every molecule would correspond to a different partitioning depending on its self-consistent electron density. In contrast, the DTNN approach learns the partitioning on a large molecular dataset, generating a transferable and global ‘dressed atom’ representation of molecules in chemical space. Recalling that DTNN exhibits errors below 1 kcal mol−1, the classification shown in Fig. 3 can provide useful guidance for the chemical discovery of molecules with desired properties. Analytical gradients of the DTNN model with respect to chemical composition or  could also aid in the exploration of chemical compound space37.
could also aid in the exploration of chemical compound space37.
Energy predictions for isomers
The quantitative accuracy achieved by DTNN and its size extensivity paves the way to the calculation of configurational and conformational energy differences—a long-standing challenge for machine learning approaches7,12,13,38. The reliability of DTNN for isomer energy predictions is demonstrated by the energy distribution in Fig. 4 for molecular isomers with C7O2H10 chemical formula (a total of 6,095 isomers in the GDB-9 data set).
Training a common model for chemical as well as conformational freedoms requires a more complex model. Furthermore, it comes with technical challenges like sampling and multiscale issues since the MD trajectories form clusters of small variation within the chemical compound space. As a proof of principle, we trained the DTNN to predict various MD trajectories of the C7O2H10 isomers. To this end, we calculated short MD trajectories of 5,000 steps each for 113 randomly picked isomers as well as consistent total energies for all equilbrium structures. The training set is composed of all isomers in equilibrium as well as 50% of each MD trajectory. The remaining MD calculations are used for validation and testing. Despite the added complexity, our model achieves a mean absolute error of 1.7 kcal mol−1.
Discussion
DTNNs provide an efficient way to represent chemical environments allowing for chemically accurate predictions. To this end, an implicit, atom-centered basis is learned from reference calculations. Employing this representation, atoms can be embedded in their chemical environment within a few refinement steps. Furthermore, DTNNs have the advantage that the embedding is built recursively from pairwise distances. Therefore, all necessary invariances (translation, rotation, permutation) are guaranteed to be exploited by the model. In addition, the learned embedding can be used to generate alchemical reaction paths (Supplementary Fig. 5).
In previous approaches, potential-energy surfaces were constructed by fitting many-body expansions with neural networks39,40,41. However, these methods require a separate NN for each non-equivalent many-body term in the expansion. Since DTNN learns a common basis in which the atom interact, higher-order interactions can obtained more efficiently without separate treament.
Approaches like smooth overlap of atomic positions16,17 or manually crafted atom-centered symmetry functions18,19,42 are, like DTNN, based on representing chemical environments. All these approaches have in common that size-extensivity regarding the number of atoms is achieved by predicting atomic energy contributions using a non-linear regression method (for example, neural networks or kernel ridge regression). However, the previous approaches have a fixed set of basis functions describing the atomic environments. In contrast, DTNNs are able to adapt to the problem at hand in a data-driven fashion. Beyond the obvious advantage of not having to manually select symmetry functions and carefully tune hyper-parameters of the representation, this property of the DTNN makes it possible to gain quantum-chemical insights by analysing the learned representation.
Obviously, more work is required to extend this predictive power for larger molecules, where the DTNN model will have to be combined with a reliable model for long-range interatomic (van der Waals) interactions. The intrinsic interpolation smoothness achieved by the DTNN model can also be used to identify molecules with peculiar electronic structure. Supplementary Fig. 6 shows a list of molecules with the largest DTNN errors compared with reference DFT calculations. It is noteworthy that most molecules in this figure are characterized by unconventional bonding and the electronic structure of these molecules has potential multi-reference character. The large prediction errors could stem from these molecules being not sufficiently represented by the training data. On the other hand, DTNN predictions might turn out to be closer to the correct answer because of its smooth interpolation in chemical space. Higher-level quantum-chemical calculations would be required to investigate this interesting hypothesis in the future.
We have proposed and developed a deep tensor neural network that enables understanding of quantum-chemical many-body systems beyond properties contained in the training dataset. The DTNN model is scalable with molecular size, efficient, and achieves uniform accuracy of 1 kcal mol−1 throughout compositional and configuration space for molecules of intermediate size. The DTNN model leads to novel insights into chemical systems, a fact that we illustrated on the example of relative aromatic ring stability, local molecular chemical potentials, relative isomer energies and the identification of molecules with peculiar electronic structure.
Many avenues remain for improving the DTNN model on multiple fronts. Among these we mention the extension of the model to increasingly larger molecules, predicting atomic forces and frequencies, and non-extensive electronic and optical properties. We propose the DTNN model as a versatile framework for understanding complex quantum-mechanical systems based on high-throughput electronic structure calculations.
Methods
Reference data sets
We employ two subsets of the GDB database34, referred to in this paper as GDB-7 and GDB-9. GDB-7 contains 7,211 molecules with up to seven heavy atoms out of the elements C, N, O, S and Cl, saturated with hydrogen12. Similarly, GDB-9 includes 133,885 molecules with up to 9 heavy atoms out of C, O, N, F (ref. 36). Both data sets include calculations of atomization energies employing density-functional theory43 with the PBE0 (ref. 44) and B3LYP (ref. 45, 46, 47, 48, 49) exchange-correlation potential, respectively.
The molecular dynamics trajectories are calculated at a temperature of 500 K and resolution of 0.5 fs using density-functional theory with the PBE exchange-correlation potential50. The data sets for benzene, toluene, malonaldehyde and salicylic acid consist of 627, 442, 993 and 320 k time steps, respectively. In the presented experiments, we predict the potential energy of the MD geometries.
Details on the deep tensor neural network model
The molecular energies of the various data sets are predicted using a deep tensor neural network. The core idea is to represent atoms in the molecule as vectors depending on their type and to subsequently refine the representation by embedding the atoms in their neighbourhood. This is done in a sequence of interaction passes, where the atom representations influence each other in a pair-wise fashion. While each of these refinements depends only on the pair-wise atomic distances, multiple passes enable the architecture to also take angular information into account. Because of this decomposition of atomic interactions, an efficient representation of embedded atoms is learned following quantum-chemical principles.
In the following, we describe the deep tensor neural network step-by-step, including hyper-parameters used in our experiments.
1. Assign initial atomic descriptors
We assign an initial coefficient vector to each atom i of the molecule according to its nuclear charge Zi:

where B is the number of basis functions. All presented models use atomic descriptors with 30 coefficients. We initialize each coefficient randomly following  .
.
2. Gaussian feature expansion of the inter-atomic distances
The inter-atomic distances Dij are spread across many dimensions by a uniform grid of Gaussians

with Δμ being the gap between two Gaussians of width σ.
In our experiments, we set both to 0.2 Å. The centre of the first Gaussian μmin was set to −1, while μmax was chosen depending on the range of distances in the data (10 Å for GDB-7 and benzene, 15 Å for toluene, malonaldehyde and salicylic acid and 20 Å for GDB-9).
3. Perform T interaction passes
Each coefficient vector  , corresponding to atom i after t passes, is corrected by the interactions with the other atoms of the molecule:
, corresponding to atom i after t passes, is corrected by the interactions with the other atoms of the molecule:

Here, we model the interaction v as follows:

where the circle () represents the element-wise matrix product. The factor representation in the presented models employs 60 neurons.
4. Predict energy contributions
Finally, we predict the energy contributions Ei from each atom i. Employing two fully-connected layers, for each atom a scaled energy contribution  is predicted:
is predicted:


In our experiments, the hidden layer oi possesses 15 neurons. To obtain the final contributions,  is shifted to the mean Eμ and scaled by the s.d. Eσ of the energy per atom estimated on the training set.
is shifted to the mean Eμ and scaled by the s.d. Eσ of the energy per atom estimated on the training set.

This procedure ensures a good starting point for the training.
5. Obtain the molecular energy E=∑i Ei
The bias parameters as well as  are initially set to zero. All other weight matrices are initialized drawing from a uniform distribution according to (ref. 51). Neural network code is available.
are initially set to zero. All other weight matrices are initialized drawing from a uniform distribution according to (ref. 51). Neural network code is available.
The deep tensor neural networks have been trained for 3,000 epochs minimizing the squared error, using stochastic gradient descent with 0.9 momentum and a constant learning rate52. The final results are taken from the models with the best validation error in early stopping.
All DTNN models were trained and executed on an NVIDIA Tesla K40 GPU. The computational cost of the employed models depends on the number of reference calculations, the number of interaction passes as well as the number of atoms per molecule. The training times for all models and data sets are shown in Supplementary Table 2, ranging from 6 h for 5.768 reference calculations of GDB-7 with one interaction pass, to 162 h for 100,000 reference calculations of the GDB-9 data set with three interaction passes.
On the other hand, the prediction is instantaneous: all models predict examples from the employed data sets in <1 ms. Supplementary Fig. 7 shows the scaling of the prediction time with the number of atoms and interaction layers. Even for a molecule with 100 atoms, a DTNN with three interaction layers requires <5 ms for a prediction.
The prediction as well as the training steps scale linearly with the number of interaction passes and quadratically with the number of atoms, since the pairwise atomic distances are required for the interactions. For large molecules it is reasonable to introduce a distance cutoff. In that case, the DTNN will also scale linearly with the number of atoms.
Computing and visualizing the local potentials of the DTNN
Given a trained neural network as described in the previous section, one can extract the coefficients vectors  for each atom i and each interaction pass t for a molecule of interest. From each final representation
for each atom i and each interaction pass t for a molecule of interest. From each final representation  , the energy contribution Ei of the corresponding atom to the molecular energy can be obtained. Instead, we let the molecule act on a probe atom, described by its charge z and the pairwise distances d1,…, dn to the atoms of the molecule:
, the energy contribution Ei of the corresponding atom to the molecular energy can be obtained. Instead, we let the molecule act on a probe atom, described by its charge z and the pairwise distances d1,…, dn to the atoms of the molecule:

with  . While this is equivalent to how the coefficient vectors of the molecule are corrected, here, the molecule does not get to be influenced by the probe. Now, the energy of the probe atom is predicted as usual from the final representation
. While this is equivalent to how the coefficient vectors of the molecule are corrected, here, the molecule does not get to be influenced by the probe. Now, the energy of the probe atom is predicted as usual from the final representation  .
.
Interpreting this as a local potential  generated by the molecule, we can use the neural network to visualize the learned interactions as illustrated in Supplementary Fig. 8. The presented energy surfaces show the potential for different probe atoms plotted on an isosurface of
generated by the molecule, we can use the neural network to visualize the learned interactions as illustrated in Supplementary Fig. 8. The presented energy surfaces show the potential for different probe atoms plotted on an isosurface of  . We used Mayavi53 for the visualization of the surfaces.
. We used Mayavi53 for the visualization of the surfaces.
Data availability
The GDB-9 data set is available under the DOI 10.6084/m9.figshare.978904. All data sets used in this work are available at http://quantum-machine.org/datasets/.
Additional information
How to cite this article: Schütt, K. T. et al. Quantum-chemical insights from deep tensor neural networks. Nat. Commun. 8, 13890 doi: 10.1038/ncomms13890 (2017).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Kang, B. & Ceder, G. Battery materials for ultrafast charging and discharging. Nature 458, 190–193 (2009).
Nørskov, J. K., Bligaard, T., Rossmeisl, J. & Christensen, C. H. Towards the computational design of solid catalysts. Nat. Chem. 1, 37–46 (2009).
Hachmann, J. et al. The Harvard clean energy project: large-scale computational screening and design of organic photo-voltaics on the world community grid. J. Phys. Chem. Lett. 2, 2241–2251 (2011).
Pyzer-Knapp, E. O., Suh, C., Gomez-Bombarelli, R., Aguilera-Iparraguirre, J. & Aspuru-Guzik, A. What is high-throughput virtual screening? A perspective from organic materials discovery. Annu. Rev. Mater. Res. 45, 195–216 (2015).
Curtarolo, S. et al. The high-throughput highway to computational materials design. Nat. Mater. 12, 191–201 (2013).
Snyder, J. C., Rupp, M., Hansen, K., Müller, K.-R. & Burke, K. Finding density functionals with machine learning. Phys. Rev. Lett. 108, 253002 (2012).
Rupp, M., Tkatchenko, A., Muller, K.-R. & Von Lilienfeld, O. A. Fast and accurate modeling of molecular atomization energies with machine learning. Phys. Rev. Lett. 108, 058301 (2012).
Ramakrishnan, R., Dral, P. O., Rupp, M. & von Lilienfeld, O. A. Big data meets quantum chemistry approximations: the Δ-machine learning approach. J. Chem. Theory Comput. 11, 2087–2096 (2015).
Bishop, C. M. Pattern Recognition and Machine Learning Springer (2006).
Ghiringhelli, L. M., Vybiral, J., Levchenko, S. V., Draxl, C. & Scheffler, M. Big data of materials science: critical role of the descriptor. Phys. Rev. Lett. 114, 105503 (2015).
Schütt, K. et al. How to represent crystal structures for machine learning: towards fast prediction of electronic properties. Phys. Rev. B 89, 205118 (2014).
Montavon, G. et al. Machine learning of molecular electronic properties in chemical compound space. New J. Phys. 15, 095003 (2013).
Hansen, K. et al. Assessment and validation of machine learning methods for predicting molecular atomization energies. J. Chem. Theory Comput. 9, 3404–3419 (2013).
Hirn, M., Poilvert, N. & Mallat, S. Quantum energy regression using scattering transforms. Preprint at https://arxiv.org/abs/1502.02077 (2015).
Hansen, K. et al. Machine learning predictions of molecular properties: accurate many-body potentials and nonlocality in chemical space. J. Phys. Chem. Lett. 6, 2326 (2015).
Bartók, A. P., Kondor, R. & Csanyi, G. On representing chemical environments. Phys. Rev. B 87, 184115 (2013).
Bartók, A. P., Payne, M. C., Kondor, R. & Csanyi, G. Gaussian approximation potentials: the accuracy of quantum mechanics, without the electrons. Phys. Rev. Lett. 104, 136403 (2010).
Behler, J. Atom-centered symmetry functions for constructing high-dimensional neural network potentials. J. Chem. Phys. 134, 074106 (2011).
Behler, J. Neural network potential-energy surfaces in chemistry: a tool for large-scale simulations. Phys. Chem. Chem. Phys. 13, 17930–17955 (2011).
LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015).
Montavon, G., Braun, M. L. & Müller, K.-R. Kernel analysis of deep networks. J. Mach. Learn. Res. 12, 2563–2581 (2011).
Ciresan, D., Meier, U. & Schmidhuber, J. Multi-column deep neural networks for image classification. In Proc. Conference on Computer Vision and Pattern Recognition. 3642–3649 (2012).
Krizhevsky, A., Sutskever, I. & Hinton, G. E. ImageNet classification with deep convolutional neural networks. In Proc. Advances in Neural Information Processing Systems. 25, 1097–1105 (2012).
LeCun, Y. & Bengio, Y. in The Handbook of Brain Theory and Neural Networks (ed. Arbib M.A.) 255–257 (The MIT Press, Cambridge, MA, USA, 1995).
Hinton, G. et al. Deep neural networks for acoustic modeling in speech recognition: the shared views of four research groups. IEEE Signal Process. Mag. 29, 82–97 (2012).
Sainath, T. N. et al. Deep convolutional neural networks for large-scale speech tasks. Neural Netw. 64, 39–48 (2015).
Collobert, R. & Weston, J. A unified architecture for natural language processing: deep neural networks with multitask learning. In Proc. 25th International Conference on Machine Learning. 160–167 (2008).
Scarselli, F., Gori, M., Tsoi, A. C., Hagenbuchner, M. & Mon-fardini, G. The graph neural network model. IEEE Trans. Neural Netw. 20, 61–80 (2009).
Duvenaud, D. K. et al. Convolutional networks on graphs for learning molecular fingerprints. In Proc. Advances in Neural Information Processing Systems. 28, 2224–2232 (2015).
Socher, R. et al. Recursive deep models for semantic compositionality over a sentiment treebank. In Proc. of the conference on empirical methods in natural language processing (EMNLP) 1631–1642 (2013).
Sutskever, I., Martens, J. & Hinton, G. E. Generating text with recurrent neural networks. Proc. 28th Annu. Int. Conf. Mach. Learn. 1017–1024 (2011).
Socher, R., Chen, D., Manning, C. D. & Ng, A. Reasoning with neural tensor networks for knowledge base completion. In Proc. Advances in Neural Information Processing Systems. 26, 926–934 (2013).
Taylor, G. W. & Hinton, G. E. Factored conditional restricted Boltzmann machines for modeling motion style. In Proc. 26th Annual International Conference on Machine Learning. 1025–1032 (2009).
Blum, L. C. & Reymond, J.-L. 970 Million Druglike Small Molecules for Virtual Screening in the Chemical Universe Database GDB-13. J. Am. Chem. Soc. 131, 8732 (2009).
Reymond, J.-L. The chemical space project. Acc. Chem. Res. 48, 722–730 (2015).
Ramakrishnan, R., Dral, P. O., Rupp, M. & von Lilienfeld, O. A. Quantum chemistry structures and properties of 134 kilo molecules. Sci. Data 1, 140022 (2014).
von Lilienfeld, O. A. First principles view on chemical compound space: gaining rigorous atomistic control of molecular properties. Int. J. Quantum Chem. 113, 1676–1689 (2013).
De, S., Bartok, A. P., Csanyi, G. & Ceriotti, M. Comparing molecules and solids across structural and alchemical space. Phys. Chem. Chem. Phys. 18, 13754–13769 (2016).
Malshe, M. et al. Development of generalized potential-energy surfaces using many-body expansions, neural networks, and moiety energy approximations. J. Chem. Phys. 130, 184102 (2009).
Manzhos, S. & Carrington, T. Jr A random-sampling high dimensional model representation neural network for building potential energy surfaces. J. Chem. Phys. 125, 084109 (2006).
Manzhos, S. & Carrington, T. Jr Using neural networks, optimized coordinates, and high-dimensional model representations to obtain a vinyl bromide potential surface. J. Chem. Phys. 129, 224104 (2008).
Behler, J. & Parrinello, M. Generalized neural-network representation of high-dimensional potential-energy surfaces. Phys. Rev. Lett. 98, 146401 (2007).
Hohenberg, P. & Kohn, W. Inhomogeneous electron gas. Phys. Rev. 136, B864–B871 (1964).
Perdew, J. P., Ernzerhof, M. & Burke, K. Rationale for mixing exact exchange with density functional approximations. J. Chem. Phys. 105, 9982–9985 (1996).
Becke, A. D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 38, 3098–3100 (1988).
Lee, C., Yang, W. & Parr, R. G. Development of the Colle- Salvetti correlation-energy formula into a functional ofthe electron density. Phys. Rev. B 37, 785–789 (1988).
Vosko, S. H., Wilk, L. & Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: a critical analysis. Can. J. Phys. 58, 1200–1211 (1980).
Stephens, P., Devlin, F., Chabalowski, C. & Frisch, M. J. Ab initio calculation of vibrational absorption and circular dichro-ism spectra using density functional force fields. J. Phys. Chem. 98, 11623–11627 (1994).
Becke, A. d. Beckes 3 parameter functional combined with the non-local correlation LYP. J. Chem. Phys. 98, 5648 (1993).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Glorot, X. & Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proc. 13th International Conference on Artificial Intelligence and Statistics. 249–256 (2010).
LeCun, Y. A., Bottou, L., Orr, G. B. & Müller, K.-R. in Neural Networks: Tricks of the Trade 9–48Springer (2012).
Ramachandran, P. & Varoquaux, G. Mayavi: 3D visualization of scientific data. Comput. Sci. Eng. 13, 40–51 (2011).
Acknowledgements
We thank Huziel Sauceda for providing molecular dynamics trajectories for C7O2H10 isomers. K.T.S. and K.R.M. thank the Einstein Foundation for generously funding the ETERNAL project. Additional support was provided by the DFG (MU 987/20-1) and the Federal Ministry of Education and Research (BMBF) for the Berlin Big Data Center BBDC (01IS14013A). K.R.M. gratefully acknowledges the BK21 program funded by Korean National Research Foundation grant (No. 2012-005741). Part of this research was performed while the authors were visiting the Institute for Pure and Applied Mathematics (IPAM), which is supported by the National Science Foundation (NSF).
Author information
Authors and Affiliations
Contributions
K.T.S. conceived the DTNN, performed analyses and prepared the figures, K.T.S., F.A., K.R.M. and A.T. developed the theory, K.R.M. and A.T. designed the analyses, S.S. helped with the MD predictions, K.T.S., K.R.M. and A.T. wrote the paper. All authors discussed results and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures, Supplementary Tables, Supplementary Discussion and Supplementary Methods (PDF 3753 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Schütt, K., Arbabzadah, F., Chmiela, S. et al. Quantum-chemical insights from deep tensor neural networks. Nat Commun 8, 13890 (2017). https://doi.org/10.1038/ncomms13890
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms13890
This article is cited by
-
Materials descriptors of machine learning to boost development of lithium-ion batteries
Nano Convergence (2024)
-
Enhancing geometric representations for molecules with equivariant vector-scalar interactive message passing
Nature Communications (2024)
-
Enhanced matrix inference with Seq2seq models via diagonal sorting
Scientific Reports (2024)
-
Quantum Machine Learning for Computational Methods in Engineering: A Systematic Review
Archives of Computational Methods in Engineering (2024)
-
Advances of machine learning in materials science: Ideas and techniques
Frontiers of Physics (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.




 =3.8 Å−2 (the index i is used to sum over all atoms of the corresponding molecule). The molecules shown are (in order from top to bottom of the figure): benzene, toluene, salicylic acid and malondehyde. Atom colouring: carbon=black, hydrogen=white, oxygen=red.
=3.8 Å−2 (the index i is used to sum over all atoms of the corresponding molecule). The molecules shown are (in order from top to bottom of the figure): benzene, toluene, salicylic acid and malondehyde. Atom colouring: carbon=black, hydrogen=white, oxygen=red.
