Abstract
A hallmark of the iron-based superconductors is the strong coupling between magnetic, structural and electronic degrees of freedom. However, a universal picture of the normal state properties of these compounds has been confounded by recent investigations of FeSe where the nematic (structural) and magnetic transitions appear to be decoupled. Here, using synchrotron-based high-energy x-ray diffraction and time-domain Mössbauer spectroscopy, we show that nematicity and magnetism in FeSe under applied pressure are indeed strongly coupled. Distinct structural and magnetic transitions are observed for pressures between 1.0 and 1.7 GPa and merge into a single first-order transition for pressures ≳1.7 GPa, reminiscent of what has been found for the evolution of these transitions in the prototypical system Ba(Fe1−xCox)2As2. Our results are consistent with a spin-driven mechanism for nematic order in FeSe and provide an important step towards a universal description of the normal state properties of the iron-based superconductors.
Similar content being viewed by others
Introduction
Unconventional superconductivity is generally believed to be mediated by fluctuations associated with ordering (magnetic, orbital or charge) found in the normal state of the material1,2,3. For the high-temperature iron-based superconductors, a leading candidate is the ubiquitous stripe-like antiferromagnetic (AFM) fluctuations associated with the magnetic ordering in the normal state. In some scenarios, these same spin fluctuations also lead to nematic electronic order, identified by a tetragonal-to-orthorhombic (T–OR) structural transition4,5. In this context, nematicity corresponds to orientational order between two AFM sublattices that are only weakly coupled because of frustration that arises from large next-nearest-neighbour magnetic interactions6,7,8. However, the magnetic origin of nematicity has been recently challenged by the unusual properties of FeSe9,10,11,12,13,14,15.
For most iron-based superconductors, including AFe2As2 (A=Ca, Sr, Ba), RFeAsO (R=rare earth) and NaFeAs, stripe-like AFM order and nematic order, in the form of a T–OR transition, occur either simultaneously or in relatively close proximity in temperature, and both can be tuned by doping or applied pressure. At ambient pressure, FeSe undergoes a T–OR transition at a temperature of Ts=90 K, but no ordered AFM state has been observed16. However, muon spin-resonance (μSR) measurements on polycrystalline samples have demonstrated the emergence of magnetic order in FeSe under applied pressures greater than ∼0.8 GPa (refs 17, 18), and the magnetic transition temperature, Tm, increases with pressure whereas the structural transition is suppressed19,20,21,22. Furthermore, superconductivity in FeSe shows a four-fold increase to a transition temperature of Tc=37 K under pressure23, accompanying the increase of Tm19,20,22. Taken together, the absence of magnetic order in the presence of nematic order at ambient pressure and the opposing evolutions of magnetic and nematic order with pressure, call into question the notion of a cooperative relation between magnetism and structure as the origin of the nematic order in FeSe9,10,11,12,13,14,15.
Electrical resistivity measurements under applied pressure provide valuable information regarding the existence of phase transitions in the pressure–temperature phase space20,21,22, but microscopic measurements under pressure are required to fully elucidate the underlying nature of the transitions, the associated order parameters and the relationship between the magnetism and structure of FeSe. Although direct microscopic information concerning the magnetic structure is best obtained using neutron diffraction, several previous measurements have been unsuccessful in detecting the expected small ordered magnetic moment18,22. Therefore, we have used both high-energy x-ray diffraction (HE-XRD) and time-domain Mössbauer spectroscopy through nuclear forward scattering (NFS) to study the structural and magnetic transitions in single-crystalline FeSe under pressure. Distinct structural and magnetic transitions, and a strong cooperative coupling of the respective order parameters are observed for pressures between 1.0 and 1.7 GPa. The transitions merge into a single first-order phase line for pressures >1.7 GPa. The evolution of the phase lines and the order parameters is reminiscent of the prototypical doped system Ba(Fe1−xCox)2As2 and is consistent with a spin-driven mechanism for nematic order also in FeSe. Our results broaden the base for a universal description of the magnetic, structural and electronic properties of the iron-based superconductors.
Results
HE-XRD and NFS measurements
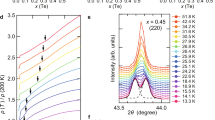
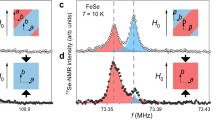
The essential results of our study are summarized in Fig. 1. Figure 1a shows that FeSe undergoes a continuous T–OR transition at ambient pressure at Ts=90 K. This is observed as a splitting of the (HH0) Bragg peaks related to the in-plane orthorhombic lattice parameters aOR and bOR. At an applied pressure of 1.5 GPa (Fig. 1e), this structural transition is suppressed to Ts=32 K. However, as the temperature is further lowered there is a subsequent abrupt increase of the splitting at 19 K. When the pressure is increased to 1.7 GPa only the discontinuous T–OR transition remains (Fig. 1f), and Ts increases to 35 K at 3.1 GPa (Fig. 1g). To correlate the features observed in the HE-XRD measurements with the evolution of the magnetism in FeSe, Fig. 1c,d show the NFS (time-domain Mössbauer spectra) at two different pressures, P=2.5 and 4.0 GPa. The small hyperfine field associated with magnetic ordering in FeSe is quite challenging for conventional Mössbauer spectroscopy23, but is readily observed in the data from our NSF measurements. The distinctive feature in these spectra is the minimum at intermediate delay times, which is determined by a convolution of the magnetic hyperfine field, quadrupolar splitting and effective sample thickness (see the ‘Methods’ section). Our fits to these spectra find that the shift in the minima at ∼30 K (P=2.5 GPa) and 40 K (P=4 GPa) is attributable to the presence of a hyperfine field at these temperatures and pressures, which confirms the onset of magnetic order in FeSe under pressure.
(a,e–g) Show the evolution of the in-plane lattice parameters at various pressures determined from the splitting of the tetragonal (HH0) Bragg peaks. The colour corresponds to detector intensities integrated over the transverse scattering directions. (b) Shows a photograph of the content of the diamond anvil pressure cell used for these measurements including the FeSe single crystal, and ruby and silver pressure indicators. (c,d) Display the time-domain 57Fe Mössbauer spectra at pressures P=2.5 and 4 GPa, respectively, with these data sets vertically offset for clarity. Grey lines are fits to the data.
Coupled first-order structural and magnetic transitions
The evolution of the structural order parameter, determined from fits to the HE-XRD data, and the evolution of the magnetic hyperfine field are shown in Fig. 2 and summarized in the pressure–temperature phase diagram of Fig. 3. These data provide insight into the relationship between structure and magnetism in FeSe under pressure. At ambient pressure, the orthorhombic distortion  displays a smooth temperature dependence characteristic of a second-order phase transition (Fig. 2a). Starting from ∼1.0 GPa, however, we observe a small discontinuous increase in δ at ∼19 K (see the inset of Fig. 2a), which is very distinct at P=1.5 GPa and higher applied pressures, as shown in Fig. 2c. Similar measurements of the canonical BaFe2As2-type iron-based superconductors clearly established that this discontinuous increase in the orthorhombicity was associated with strong magnetoelastic coupling and a transition to stripe-like magnetic order24,25. For FeSe, the magnetic ordering temperature obtained in the μSR measurements17 on polycrystalline samples is also consistent with the first-order structural transition measured by HE-XRD on our single-crystal sample. In Fig. 2b we show the evolution of the hyperfine field, Hhf, extracted from fits to our single-crystal NFS data measured at applied pressures of P=2.5 and 4.0 GPa (Fig. 1c,d). The relatively small saturated values for Hhf of ∼2.5 and 3.0 T, respectively, correspond to a small ordered moment on the order of 0.2 μB/Fe, consistent with the estimates from the previous μSR experiments18 and explain the difficulty in detecting a magnetic signal in earlier conventional Mössbauer measurements23. We also find that Tm and the saturation value of Hhf increase with increasing pressure, consistent with the previous μSR studies17,18. Although the density of data points is rather low, Fig. 2b suggests that the NFS spectra at P=4.0 GPa is consistent with a strong discontinuous transition, whereas the magnetic transition at 2.5 GPa could be described as weakly first-order.
displays a smooth temperature dependence characteristic of a second-order phase transition (Fig. 2a). Starting from ∼1.0 GPa, however, we observe a small discontinuous increase in δ at ∼19 K (see the inset of Fig. 2a), which is very distinct at P=1.5 GPa and higher applied pressures, as shown in Fig. 2c. Similar measurements of the canonical BaFe2As2-type iron-based superconductors clearly established that this discontinuous increase in the orthorhombicity was associated with strong magnetoelastic coupling and a transition to stripe-like magnetic order24,25. For FeSe, the magnetic ordering temperature obtained in the μSR measurements17 on polycrystalline samples is also consistent with the first-order structural transition measured by HE-XRD on our single-crystal sample. In Fig. 2b we show the evolution of the hyperfine field, Hhf, extracted from fits to our single-crystal NFS data measured at applied pressures of P=2.5 and 4.0 GPa (Fig. 1c,d). The relatively small saturated values for Hhf of ∼2.5 and 3.0 T, respectively, correspond to a small ordered moment on the order of 0.2 μB/Fe, consistent with the estimates from the previous μSR experiments18 and explain the difficulty in detecting a magnetic signal in earlier conventional Mössbauer measurements23. We also find that Tm and the saturation value of Hhf increase with increasing pressure, consistent with the previous μSR studies17,18. Although the density of data points is rather low, Fig. 2b suggests that the NFS spectra at P=4.0 GPa is consistent with a strong discontinuous transition, whereas the magnetic transition at 2.5 GPa could be described as weakly first-order.
(a,c) Plot the orthorhombicity,  , as a function of temperature at various pressures. Error bars indicate 2σ, the fitting error. The inset in a, shows a magnified view of the data close to the discontinuous change in δ near 19 K. A coexistence region for the orthorhombic and tetragonal phases is observed at pressures P=1.7 and 3.1 GPa as indicated by open symbols and vertical lines. The inset of c, shows the relative integrated intensities of the tetragonal (T) and orthorhombic (OR) phases on warming and cooling respectively, at P=1.7 GPa. Any thermal hysteresis is smaller than the point spacing (0.2 K), whereas the coexistence temperature region spans 1.5 K. (b) Displays the magnetic hyperfine field Hhf derived from CONUSS fits37 of the NFS data in Figs 1c,d. The error bars were estimated from fits to the data in the paramagnetic phase and include a 2% fitting error.
, as a function of temperature at various pressures. Error bars indicate 2σ, the fitting error. The inset in a, shows a magnified view of the data close to the discontinuous change in δ near 19 K. A coexistence region for the orthorhombic and tetragonal phases is observed at pressures P=1.7 and 3.1 GPa as indicated by open symbols and vertical lines. The inset of c, shows the relative integrated intensities of the tetragonal (T) and orthorhombic (OR) phases on warming and cooling respectively, at P=1.7 GPa. Any thermal hysteresis is smaller than the point spacing (0.2 K), whereas the coexistence temperature region spans 1.5 K. (b) Displays the magnetic hyperfine field Hhf derived from CONUSS fits37 of the NFS data in Figs 1c,d. The error bars were estimated from fits to the data in the paramagnetic phase and include a 2% fitting error.
Phase regions are labelled with the orthorhombic (OR), magnetic (M) and superconducting (SC) ordered states. The transition temperatures obtained from the present single-crystal HE-XRD measurements (red symbols) and fits of the NFS data (blue symbols, with error bars estimated from the width of the temperature steps in the measurement). The grey erect triangles denote transition temperatures inferred from the resistivity measurements21 on samples from the same batch used for the diffraction measurements and grey inverted triangles denote the measured superconducting transition temperature from previous work19. Thick lines in the figure represent first-order phase transitions and thin lines correspond to second-order phase transitions. The dashed line shows a tentative extrapolation. The insets to the figure show representative two-dimensional diffraction data in the respective pressure–temperature region demonstrating the splitting of the tetragonal (660) Bragg peak in the orthorhombic phase.
Discussion
Most importantly, the HE-XRD data show that the T–OR transition does not vanish above 1.7 GPa where Ts, as inferred from resistivity measurements, would extrapolate to zero13,20. Rather, the abrupt onset of the orthorhombicity and the significant coexistence range of the tetragonal and orthorhombic phases (inset of Fig. 2c) demonstrate that the structural and magnetic transitions merge to a simultaneous first-order magneto-structural transition as shown in Fig. 3 and also found, for example, in the CaFe2As2 parent compound26. Further, our HE-XRD measurements show that the magnetic order in FeSe breaks the tetragonal symmetry of the lattice in the same manner as the ubiquitous stripe-type magnetic order in the other iron-based materials. To our knowledge, no other AFM order observed in iron-based superconductors or magnetic structures proposed for FeSe27 break the tetragonal symmetry in this specific way.
The HE-XRD and NFS results for FeSe demonstrate that all features concerning the normal state structure and magnetism, and their coupling, are very similar to other iron-based superconductors, but differ in the details of the temperature and pressure dependencies of the transitions. These results are consistent with a spin-driven mechanism for nematic ordering in FeSe. In Fig. 4, we compare the schematic phase diagrams of BaFe2As2 and FeSe with trends derived from recent theoretical studies of spin-driven nematicity5. Figure 4a sketches the sequence of structural and magnetic phase transitions for BaFe2As2 as a function of doping. For Co substitution for Fe in BaFe2As2 (electron doping), the magnetic and structural transitions separate in temperature and both Ts and Tm decrease with increased substitution24. On the other hand, for hole doping, the magnetic and structural transitions are concomitant and decrease in temperature with increased doping. The pressure–temperature diagram for FeSe in Fig. 4b also mirrors the compositional phase diagram described by Fernandes et al.5. The character of the phase transitions and their evolution with applied pressure, determined from our measurements, are consistent with this diagram, although Ts increases as pressure is lowered, in contrast to the predicted decrease. One must, however, consider the relative strengths of the interactions in such models5 and how these interactions evolve with pressure. In particular, a stiffening of the elastic constants with increasing pressure can result in a decrease in Ts relative to its value at ambient pressure. Similarly, an increase in the magnetic interaction, indicated by the increase in the magnetic ordering temperature and ordered magnetic moment with increasing pressure, can push Ts,m for the coupled magneto-structural transition to a higher temperature.
For both panels the blue lines represent magnetic transitions, the red lines denote structural transitions and the violet lines represents the joint magneto-structural transition. The grey lines show the trends noted in the spin-driven nematic theory5 which differ from those found in experiments. Thick lines denote first-order transitions, whereas the thinner lines denote second-order transitions. For a, the control parameter is partial element substitution (doping) for the case of BaFe2As2. For b, the control parameter is pressure for the case of FeSe. Ts, Ts*,m and Ts,m denote the structural transition temperature, the magnetic ordering temperature associated with the discontinuous change in the orthorhombicity, and the joint structural and magnetic transition temperature, respectively.
The origin of the large difference between Ts and Tm at low pressures remains an outstanding question, as well as the presence of nematic order in the absence of magnetic order at ambient pressure. Nevertheless, we note that this is not qualitatively different from the Ba(Fe1−xCox)2As2 system in which there is a compositional range, close to x=0.06, where the nematic order is established at ∼30 K in the absence of any magnetic order4. Several possible explanations within a spin-driven scenario have been discussed. One possibility is, for example, that the magnetic transition is suppressed relative to the structural one via frustration27,28. However, other scenarios regarding the underlying mechanism for nematicity in FeSe have been put forward15,29,30,31 and the HE-XRD and NFS results presented here provide an important benchmark for further theoretical work.
Methods
Sample preparation
The FeSe single crystals were prepared using KCl/AlCl3 chemical-vapour transport32 and were thoroughly characterized in previous studies21,33. Both transition temperatures, Ts and Tm, were clearly observed by resistivity measurements under pressure21, which facilitates a mapping of the phase diagram20,21,22 and supports the high-quality of our single crystals. The batch used for the HE-XRD experiment was characterized with DC magnetization and electrical resistivity measurements, and yielded sharp superconducting transitions at Tc=8.7–8.8 K at ambient pressure. Samples for the NFS experiment were prepared similarly34 using 94% isotopically pure 57Fe, and had Tc values between 8.5–8.8 K.
High-Energy X-ray Diffraction
HE-XRD measurements were performed on the six-circle diffractometer at station 6-ID-D at the Advanced Photon Source, using 100.3 keV x-rays and a beam size of 100 × 100 μm2. A sample with dimensions 120 × 120 × 20 μm3 was loaded into a membrane-driven copper–beryllium diamond anvil cell (DAC). A tungsten gasket with an initial thickness of 120 μm was pre-indented to a thickness of 70 μm, and a 660 μm hole was laser-drilled to accommodate the sample and pressure calibrants (ruby spheres and silver foil), as shown in Fig. 1b. Helium gas was used as the pressure-transmitting medium and loaded at P=0.5 GPa. The pressure was initially determined by the fluorescence lines from ruby spheres at ambient temperature, and, during the diffraction measurements, was determined in situ by analyzing selected Bragg peaks from the silver foil. The DAC was mounted on the cold finger of a He closed-cycle refrigerator and temperature-dependent measurements were performed between T=5 and 300 K for various pressures. The pressure was always changed at temperatures well above 120 K. Extended regions of selected reciprocal lattice planes and the powder diffraction pattern of silver were recorded by a MAR345 image plate system positioned 1.474 m behind the DAC, as the DAC was rocked by up to ±3.2° about two independent axes perpendicular to the incident x-ray beam. High-resolution diffraction patterns of selected Bragg reflections were also recorded by using a Pixirad-1 detector positioned 1.397 m behind the DAC while rocking around one of the two axes perpendicular to the x-ray beam. The images in Fig. 3 show typical examples of diffraction patterns measured using the Pixirad-1 detector, and demonstrate the excellent mosaic of the single crystal under applied pressure, as evidenced by the well-split pattern of the (HH0) Bragg peaks (in tetragonal notation) due to the orthorhombic distortion35. The orthorhombic lattice parameters were determined by fitting the Bragg peak positions after integrating the data over the transverse scattering directions. This procedure was used for both the data recorded by the Pixirad-1 detector and the data recorded by the MAR345 image plate system.
Nuclear forward scattering
In NFS, highly monochromatic synchrotron radiation from an electron bunch excites the 57Fe nuclei in the sample and the decay curve is measured as a function of time. In the presence of a hyperfine interaction that splits the 57Fe nuclear energy levels, oscillations in the scattered intensity with time (quantum beats) are observed and can be directly compared with conventional Mössbauer spectroscopy36. NFS spectra were collected at beamline 16-ID-D at the Advanced Photon Source with an incident energy monochromated to the 57Fe nuclear resonance at 14.4125, keV, with a resolution of 2 meV, and a cross-section of 35 × 50 μm2 of the beam. A 57FeSe single crystal of dimensions 50 × 50 × 18 μm3 was loaded into a membrane-driven copper–beryllium DAC with 600 μm culet anvils, which allowed us to collect NFS data at P=2.5 and 4.0 GPa. A non-magnetic Cu–Be gasket was pre-indented to 55 μm thickness, and a hole of diameter 270 μm was laser-drilled to accommodate the sample and pressure calibrant (ruby spheres). Helium was loaded as the pressure-transmitting medium to enable hydrostatic pressure conditions. The DAC was mounted on the cold finger of a helium-flow cryostat, which achieved temperatures down to T=11 K. The intensity of the resonantly scattered photons in the forward direction, with 153.4 ns separation between the individual bunches, were recorded by an Avalanche Photo Diode detector. The program CONUSS37 was used to analyze the spectra and to determine the magnitude of the hyperfine field. The NFS spectrum at ambient temperature was well modelled without a magnetic hyperfine field, fitting only the effective sample thickness and quadrupolar splitting, which yielded a value of 0.20(5) mm s−1 at P=0.8 GPa consistent with earlier reports23. The low-temperature spectra were satisfactorily fit by including a hyperfine magnetic field. The two angles defining the direction of the hyperfine magnetic field with respect to the incident beam were also determined in addition to the (slightly pressure and temperature dependent) effective thickness of the sample. The values for the quadrupolar splitting were fixed to 0.15 and 0.20 mm s−1 at P=2.5 and 4.0 GPa, respectively.
Data availability
All relevant data are available from the corresponding authors upon request.
Additional information
How to cite this article: Kothapalli, K. et al. Strong cooperative coupling of pressure-induced magnetic order and nematicity in FeSe. Nat. Commun. 7:12728 doi: 10.1038/ncomms12728 (2016).
References
Johnston, D. C. The puzzle of high temperature superconductivity in layered iron pnictides and chalcogenides. Adv. Phys. 59, 803–1061 (2010).
Stewart, G. R. Superconductivity in iron compounds. Rev. Mod. Phys. 83, 1589–1652 (2011).
Si, Q., Yu, R. & Abrahams, E. High-temperature superconductivity in iron pnictides and chalcogenides. Nat. Rev. Mater. 1, 16017 (2016).
Nandi, S. et al. Anomalous suppression of the orthorhombic lattice distortion in superconducting Ba(Fe1−xCox)2As2 single crystals. Phys. Rev. Lett. 104, 057006 (2010).
Fernandes, R. M., Chubukov, A. V. & Schmalian, J. What drives nematic order in iron-based superconductors? Nat. Phys. 10, 97–104 (2014).
Chandra, P., Coleman, P. & Larkin, A. I. Ising transition in frustrated Heisenberg models. Phys. Rev. Lett. 64, 88–91 (1990).
Yildirim, T. Origin of the 150-K anomaly in LaFeAsO: competing antiferromagnetic interactions, frustration, and a structural phase transition. Phys. Rev. Lett. 101, 057010 (2008).
Si, Q. & Abrahams, E. Strong correlations and magnetic frustration in the high Tc iron pnic-tides. Phys. Rev. Lett. 101, 076401 (2008).
Watson, M. D. et al. Emergence of the nematic electronic state in FeSe. Phys. Rev. B 91, 155106 (2015).
Böhmer, A. E. et al. Origin of the tetragonal-to-orthorhombic phase transition in FeSe: a combined thermodynamic and NMR study of nematicity. Phys. Rev. Lett. 114, 027001 (2015).
Baek, S.-H. et al. Orbital-driven nematicity in FeSe. Nat. Mater. 14, 210–214 (2015).
Massat, P. et al. Charge induced nematicity in FeSe. Preprint at http://arxiv.org/abs/ 1603.01492 (2016).
Wang, Q. et al. Magnetic ground state of FeSe. Preprint at http://arxiv.org/abs/1511.02485 (2015).
Shamoto, S. et al. Spin nematic susceptibility studied by inelastic neutron scattering in FeSe. Preprint at http://arxiv.org/abs/1511.04267 (2015).
Yu, R. & Si, Q. Antiferroquadrupolar and Ising-nematic orders of a frustrated bilinear-biquadratic Heisenberg model and implications for the magnetism of FeSe. Phys. Rev. Lett. 115, 116401 (2015).
McQueen, T. M. et al. Tetragonal-to-orthorhombic structural phase transition at 90 K in the superconductor FeL01Se. Phys. Rev. Lett. 103, 057002 (2009).
Bendele, M. et al. Pressure induced static magnetic order in superconducting FeSe1−x . Phys. Rev. Lett. 104, 087003 (2010).
Bendele, M. et al. Coexistence of superconductivity and magnetism in FeSe1−x under pressure. Phys. Rev. B 85, 064517 (2012).
Miyoshi, K. et al. Enhanced superconductivity on the tetragonal lattice in FeSe under hydrostatic pressure. J. Phys. Soc. Jpn. 83, 013702 (2014).
Terashima, T. et al. Pressure-induced antiferromagnetic transition and phase diagram in FeSe. J. Phys. Soc. Jpn. 84, 063701 (2015).
Kaluarachchi, U. S. et al. Nonmonotonic pressure evolution of the upper critical field in superconducting FeSe. Phys. Rev. B 93, 064503 (2016).
Sun, J. P. et al. Dome-shaped magnetic order competing with high-temperature superconductivity at high pressures in FeSe. Nat. Commun. 7, 12146 (2016).
Medvedev, S. et al. Electronic and magnetic phase diagram of (3-Fe1.01Se with superconductivity at 36.7 K under pressure. Nat. Mat 8, 630–633 (2009).
Kim, M. G. et al. Character of the structural and magnetic phase transitions in the parent and electron-doped BaFe2As2 compounds. Phys. Rev. B 83, 134522 (2011).
Pajerowski, D. M., Rotundu, C. R., Lynn, J. W. & Birgeneau, R. J. Magnetic neutron diffraction study of Ba(Fe1−xCox)2As2 critical exponents through the tricritical doping. Phys. Rev. B 87, 134507 (2013).
Ni, N. et al. First-order structural phase transition in CaFe2As2 . Phys. Rev. B 78, 014523 (2008).
Glasbrenner, J. K. et al. Effect of magnetic frustration on nematicity and superconductivity in iron chalcogenides. Nat. Phys. 11, 953–958 (2015).
Chubukov, A. V., Fernandes, R. M. & Schmalian, J. Origin of nematic order in FeSe. Phys. Rev.B 91, 201105 (2015).
Chubukov, A. V., Khodas, M. & Fernandes, R. M. Magnetism, superconductivity, and spontaneous orbital order in iron-based superconductors: who comes first and why? Preprint at http://arxiv.org/abs/1602.05503 (2016).
Fanfarillo, L. et al. Orbital-dependent Fermi surface shrinking as a fingerprint of nematicity in FeSe. Preprint at http://arxiv.org/abs/1605.02482 (2016).
Hu, W.-J. et al. Frustrated magnetism and quantum transitions of nematic phases in FeSe. Preprint at http://arxiv.org/abs/1606.01235 (2016).
Böhmer, A. E. et al. Lack of coupling between superconductivity and orthorhombic distortion in stoichiometric single-crystalline FeSe. Phys. Rev. B 87, 180505 (2013).
Tanatar, M. A. et al. Origin of the resistivity anisotropy in the nematic phase of FeSe. Preprint at http://arxiv.org/abs/1511.04757 (2015).
Böhmer, A. E., Taufour, V., Straszheim, W. E., Wolf, T. & Canfield, P. C. Variation of transition temperatures and residual resistivity ratio in vapor-grown FeSe. Preprint at http://arxiv.org/abs/1606.00500 (2016).
Tanatar, M. A. et al. Direct imaging of the structural domains in the iron pnictides AFe2As2 (A = Ca, Sr, Ba). Phys. Rev. B 79, 180508R (2009).
Gerdau, E. & DeWaard, H. (eds). Nuclear resonant scattering of synchrotron radiation. Hyperfine Interact. 123-124, 1–879 (1999).
Sturhahn, W. CONUSS and PHOENIX: Evaluation of nuclear resonant scattering data. Hyperfine Interact. 125, 149–172 (2000).
Acknowledgements
The authors would like to acknowledge the assistance of D.S. Robinson, C. Benson, S. Tkachev, S.G. Sinogeikin and M. Baldini, and helpful discussions with R.J. McQueeney and R.M. Fernandes. Work at the Ames Laboratory was supported by the Department of Energy, Basic Energy Sciences, Division of Materials Sciences & Engineering, under Contract No. DE-AC02-07CH11358. AEB acknowledges support from the Helmholtz Association via PD-226. This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. HPCAT operations are supported by DOE-NNSA under Award No. DE-NA0001974 and DOE-BES under Award No. DE-FG02-99ER45775, with partial instrumentation funding by NSF. Use of the COMPRES-GSECARS gas loading system was supported by COMPRES under NSF Cooperative Agreement EAR 11-57758 and by GSECARS through NSF grant EAR-1128799 and DOE grant DE-FG02-94ER14466.
Author information
Authors and Affiliations
Contributions
K.K., A.E.B., S.L.B., P.C.C., A.K. and A.I.G. designed the measurements; A.E.B. and V.T. grew the samples; K.K., A.E.B., W.T.J., B.G.U., P.D., A.S., D.S.R. and A.K. performed and analyzed the HE-XRD measurements; K.K., A.E.B., W.T.J., Y.X., E.A. and A.K. performed and analyzed the NFS measurements; A.I.G., A.K., A.E.B., K.K. and P.C.C. drafted the manuscript and all authors participated in the writing and review of the final draft.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no conflict of interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Kothapalli, K., Böhmer, A., Jayasekara, W. et al. Strong cooperative coupling of pressure-induced magnetic order and nematicity in FeSe. Nat Commun 7, 12728 (2016). https://doi.org/10.1038/ncomms12728
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms12728
This article is cited by
-
Order from disorder phenomena in BaCoS2
Communications Physics (2024)
-
Nematic fluctuations in an orbital selective superconductor Fe1+yTe1−xSex
Communications Physics (2023)
-
Magnetic Transition at High Temperature on FeSe0.88 Superconductor
Journal of Superconductivity and Novel Magnetism (2023)
-
Crossover in Low-temperature Ground State of Fe(Se,Te) Compounds
Journal of Superconductivity and Novel Magnetism (2023)
-
Lattice-shifted nematic quantum critical point in FeSe1−xSx
npj Quantum Materials (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.