Abstract
Although the freezing of liquids and melting of crystals are fundamental for many areas of the sciences, even simple properties like the temperature–pressure relation along the melting line cannot be predicted today. Here we present a theory in which properties of the coexisting crystal and liquid phases at a single thermodynamic state point provide the basis for calculating the pressure, density and entropy of fusion as functions of temperature along the melting line, as well as the variation along this line of the reduced crystalline vibrational mean-square displacement (the Lindemann ratio), and the liquid’s diffusion constant and viscosity. The framework developed, which applies for the sizable class of systems characterized by hidden scale invariance, is validated by computer simulations of the standard 12-6 Lennard-Jones system.
Similar content being viewed by others
Introduction
Melting is the prototypical first-order phase transition1,2,3. Its qualitative description has been textbook knowledge for a century, but it has proven difficult to give quantitatively accurate predictions. This is the case not only for the kinetics of freezing and melting, which are exciting and highly active areas of research4,5,6,7,8; there is not even a theory for calculating, for example, the entropy of fusion as a function of temperature along the melting line in the thermodynamic phase diagram.
The everyday observation that matter sticks together but is at the same time almost impossible to compress9 is modelled, for example, in the system proposed by Lennard-Jones (LJ) in 1924 (ref. 10). Here, particles interact via a pair potential that as a function of distance r is a difference of two inverse power-law terms: υLJ(r)=4ɛ((r/σ)−12−(r/σ)−6). The first term reflects the fact that the repulsive ‘Pauli’ forces are harsh and short-ranged, the negative term models the softer, longer ranged attractive van der Waals forces. The 1970s led to the development of highly successful thermodynamic perturbation and integral-equation theories for simple liquids11,12,13,14,15,16. Their main ingredient is the assumption that the structure of a dense, monatomic fluid closely resembles that of a collection of hard spheres14,16,17,18. Confirming this, the structure of melts of, for example, metallic elements near freezing is close to that of the hard-sphere system15,16,18,19. The term ‘structure’ generally refers to the entire collection of spatial equal-time density correlation functions, but our focus below is on the pair correlation function (in the form of its Fourier transform, the structure factor) as the most important structural characteristic.
Since the hard-sphere system has only a single nontrivial thermodynamic state parameter, the packing fraction, the phase diagram is basically one-dimensional, which implies that the system has a unique freezing/melting transition. On the basis of this, for simple systems one expects invariance along the freezing and melting lines of structure and dynamics in proper units, as well as of thermodynamic variables like the relative density change upon melting and the melting entropy20. Empirical freezing and melting rules, which follow from the hard-sphere melting picture and are fairly well obeyed for most simple systems, include the fact that the ratio between the crystalline root-mean-square atomic displacement and the nearest-neighbor distance—known as the Lindemann ratio—is constant and about 0.1 along the melting line; this is the famous Lindemann melting criterion from 1910 (refs 20, 21, 22, 23, 24, 25). In the hard-sphere model the Lindemann ratio is universal at melting because, as mentioned, there is just a single melting point. Thus, for systems well described by the hard-sphere model the Lindemann ratio is predicted to be invariant along the melting line. Other empirical rules, which are predicted by the hard-sphere picture and reasonably well obeyed by many systems, include the facts that in properly reduced units the liquid’s self-diffusion constant and viscosity are invariant along the freezing line26,27, the Hansen–Verlet rule17,28 that the amplitude of the first peak of the liquid static structure factor is about 2.85 at freezing, or Richard’s melting rule3 that the entropy of fusion ΔSfus is about 1.1kB (which in a more modern and accurate version is the fact that the constant-volume entropy difference across the density–temperature coexistence region is close to 0.8kB (refs 23, 29)).
The below study shows how the thermodynamics of freezing and melting for a large class of systems may be predicted to a good approximation from computer simulations carried out at a single coexistence state point. In particular, the theory developed quantifies the deviations from the above mentioned hard-sphere predicted melting-line invariants16,22,30,31,32. The theory is validated by computer simulations of the standard 12-6 LJ system.
Results
General theory
It is well-known that adding a mean-field attractive term to the hard-sphere model broadens the coexistence region, which on the other hand, narrows if the repulsive part is softened13,16,33,34,35,36. Such terms are therefore expected to modify the hard-sphere predicted invariances along the freezing and melting lines. As an illustration, Fig. 1a shows that in reduced units there is approximate identity of structure along the LJ freezing line, but the structure is not entirely invariant as seen in the inset where the dashed line marks the predicted maximum based on simulations at T0=2.0ɛ/kB, if the structure were invariant.
(a) Liquid structure factor along the freezing line37 showing results from T=0.7ɛ/kB, which is close to the triple point, to T=3.4ɛ/kB. The hard-sphere model predicts that the height of the first peak is invariant along the freezing line as indicated by the blue dashed line in the inset. Small, but systematic deviations are observed. (b) Liquid structure factor along the isomorph crossing the freezing line at temperature T0=2.0ɛ/kB (henceforth used as the liquid reference isomorph), demonstrating structural invariance to a much higher degree. This is the basis for the theory proposed in the present paper.
In order to develop a quantitative theory of freezing and melting, we take as starting point the ‘hidden scale invariance’ property of systems38 characterized by a potential-energy function U(R), where R=(r1, r2,…,rN) is the collective coordinate of the system’s N particles, which to a good approximation obeys the scaling condition.39

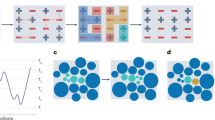
Here, λ is a scaling factor and it is understood that the sample container undergoes the same scaling as the configuration; thus λ>1 corresponds to a density decrease and λ<1 to a density increase. This form of scale invariance is exact only for systems with Euler-homogeneous interactions (plus a constant)13. It is a good approximation, however, for the condensed phases of many systems in which this property is not obvious from inspection of the analytical expression for U(R), thus the term ‘hidden scale invariance’39,40,41,42. Equation (1), which is formally equivalent to the conformal-invariance condition U(Ra)=U(Rb)⇔U(λ Ra)=U(λ Rb), implies invariance of structure and dynamics along the configurational adiabats in the phase diagram39. These lines are referred to as isomorphs42. It was very recently shown by Maimbourg and Kurchan43 that in high dimensions all pair-potential systems obey hidden scale invariance in their condensed phase. Experimentally, hidden scale invariance has been demonstrated directly and indirectly for molecular van der Waals bonded liquids and polymers44,45,46. Further evidence for the existence of isomorphs comes from computer simulations of single-component systems40,42 as well as, for example, of glass-forming mixtures47, nanoflows48, molecular models38 and molecular dynamics (MD) simulations of the dynamics of most metallic elements based on quantum-mechanical, density-functional-theory potentials49. Isomorphs have also been demonstrated in simulations of out-of-equilibrium situations like zero-temperature shear flows of glasses or nonlinear steady-state liquid flows (see, for example, ref. 38 and its references). It is important to emphasize, however, that not all condensed matter exhibits hidden scale invariance; for instance, water is a notable exception41. The general picture is that most metals and organic van der Waals bonded systems obey equation (1) to a good approximation in the condensed-phase part of their thermodynamic phase diagram, whereas systems with strong directional bonding generally do not38. The former systems are simpler than the latter because their phase diagrams are effectively one-dimensional in regard to structure and dynamics, reminiscent of the hard-sphere system. Systems with hidden scale invariance are sometimes referred to as Roskilde (R) simple35,50,51,52,53,54,55,56,57,58,59,60,61,62 to distinguish them from simple systems traditionally defined as pair-potential systems16. The theory presented below makes use of R simple systems’ almost one-dimensional phase diagrams38 and gives corrections to the hard-sphere picture of melting and freezing calculated by the first-order Taylor expansions. Figure 2 illustrates the idea.
The freezing and melting lines are both close to isomorphs along which basically everything is known because the reduced-unit structure and dynamics are invariant to a very good approximation. Properties along the freezing and melting lines are estimated via first-order Taylor expansions by moving from an isomorph to the freezing or melting line; the two reference isomorphs (a liquid and a solid one) are determined from computer simulations at T0=2.0ɛ/kB. Details are given in the ‘Methods’ section.
Along an isomorph the structure is invariant in the reduced-unit system defined42 by the length unit ρ−1/3 (ρ≡N/V is the number density and V is the system volume), the energy unit kBT (T is the temperature) and the time unit  (m is the particle mass). Figure 1b shows the LJ liquid’s static structure factor S(q) along an isomorph close to the freezing line (used below as the liquid-state reference isomorph) plotted for a range of temperatures. A comparison with Fig. 1a confirms the recent finding of Heyes and Branka32 that the freezing line is not an exact isomorph, although it is close to one.
(m is the particle mass). Figure 1b shows the LJ liquid’s static structure factor S(q) along an isomorph close to the freezing line (used below as the liquid-state reference isomorph) plotted for a range of temperatures. A comparison with Fig. 1a confirms the recent finding of Heyes and Branka32 that the freezing line is not an exact isomorph, although it is close to one.
The melting pressure as a function of temperature, pm(T), can be predicted from information obtained at a single coexistence reference state point. The details about how this works are given in the ‘Methods’ section. The argument may be summarized as follows. Recalling that the entropy as a function of density and temperature is a sum of an ideal-gas term and an ‘excess’ term Sex (ref. 16), isomorphs are the phase-diagram lines of constant excess entropy for any system obeying equation (1)39,42. A computer simulation at the liquid/solid reference state point generates a series of configurations R10,…, Rn0. Scaling each of these uniformly to density ρ one obtains configurations representative for the state point with density ρ and temperature T on the isomorph through the reference state point39 in which T is identified from the configurational temperature expression63 kBT=〈(∇U)2〉/〈∇2U〉. The average potential energy U and virial W at the state point (ρ, T) are likewise found by averaging over the scaled configurations. The key assumption here is that the canonical probabilities of the scaled configurations are identical to those of the original configurations, which follows from equation (1)39 (thus no new MD simulations are required). As shown in the ‘Methods’ section, in conjunction with the excess isochoric specific heat CVex calculated from the potential-energy fluctuations of the scaled configurations (CVex=〈(ΔU)2〉/kBT2) and the so-called density-scaling exponent  also calculated from the fluctuations (γ=〈ΔUΔW〉/〈(ΔU)2〉), one has enough information to determine the thermodynamics of freezing and melting, as well as the variation along the melting line of isomorph-invariant properties like the Lindemann ratio and the reduced-unit viscosity.
also calculated from the fluctuations (γ=〈ΔUΔW〉/〈(ΔU)2〉), one has enough information to determine the thermodynamics of freezing and melting, as well as the variation along the melting line of isomorph-invariant properties like the Lindemann ratio and the reduced-unit viscosity.
The LJ system
For LJ type systems, the general procedure described above may be implemented analytically by making use of the fact that because the structure is isomorph invariant, it is possible to calculate the variation of the average potential energy and other relevant quantities analytically along an isomorph. This is done as follows. In reduced coordinates the pair correlation function  is isomorph invariant
is isomorph invariant  . Consequently, for pairs of LJ particles at distance r the thermal average 〈r−n〉 scales with density as ρn/3 along an isomorph. Thus 〈r−n〉 ∝ ρn/3 with a proportionality constant that only depends on Sex, implying that the average potential energy U is of the form64
. Consequently, for pairs of LJ particles at distance r the thermal average 〈r−n〉 scales with density as ρn/3 along an isomorph. Thus 〈r−n〉 ∝ ρn/3 with a proportionality constant that only depends on Sex, implying that the average potential energy U is of the form64  in which
in which  is the density relative to the reference state-point density and A6(Sex)<0 derives from the attractive term of the LJ potential. Since T=(∂U/∂Sex)ρ, one has
is the density relative to the reference state-point density and A6(Sex)<0 derives from the attractive term of the LJ potential. Since T=(∂U/∂Sex)ρ, one has  . It follows that if the five quantities Sex, A12(Sex), A6(Sex),
. It follows that if the five quantities Sex, A12(Sex), A6(Sex),  and
and  are known, the excess Helmholtz free energy, U–TSex, is known along the reference isomorph. The required quantities are easily determined from reference state-point simulations (see the ‘Methods’ section)—for instance the reference state-point’s potential energy and virial give two linear equations for determining A12(Sex) and A6(Sex). Once the excess Helmholtz free energy is known along the reference isomorph, the Gibbs free energy is found by adding the ideal-gas Helmholtz free energy and the pV term (pV=NkBT+W in which the virial is given42 by
are known, the excess Helmholtz free energy, U–TSex, is known along the reference isomorph. The required quantities are easily determined from reference state-point simulations (see the ‘Methods’ section)—for instance the reference state-point’s potential energy and virial give two linear equations for determining A12(Sex) and A6(Sex). Once the excess Helmholtz free energy is known along the reference isomorph, the Gibbs free energy is found by adding the ideal-gas Helmholtz free energy and the pV term (pV=NkBT+W in which the virial is given42 by  ).
).
Comparing theory to simulation results for the LJ system
Following the above procedure, we generated two reference isomorphs for the LJ system starting from the coexistence state point with temperature T0=2.0ɛ/kB, a liquid-phase isomorph and a crystal-phase isomorph. Gibbs free energy of the liquid phase at coexistence, Gl(T), is found by utilizing the fact that the freezing line is close to an isomorph. Since (∂G/∂p)T =V, a good approximation to Gl at coexistence is

Here, pm(T) is the coexistence pressure to be determined; GlI(T) is the Gibbs-free energy, VlI(T) the volume and plI(T) the pressure along the liquid-state reference isomorph. These quantities are all known functions of the (relative) density on the isomorph henceforth denoted by  , which for temperature T is found by solving
, which for temperature T is found by solving  .
.
An analogous expression applies for the crystal’s Gibbs free energy, of course, again involving only parameters determined from reference state-point simulations. The coexistence pressure is determined by equating the liquid and solid phases’ Gibbs free energies. As shown in the ‘Methods’ section (equation (21)), this results in pm(T)(VlI(T)−VsI(T))=C1(T)+C2(T)−C3(T) in which C1(T) is the difference between UsI(T)−(T/T0)UsI(T0) and the analogous term for the liquid reference isomorph (here UsI(T) is the crystal’s potential energy along the reference isomorph), C2(T) is the difference between  and the analogous liquid term and C3(T) is the difference between (T/T0)WsI(T0) and the analogous liquid term.
and the analogous liquid term and C3(T) is the difference between (T/T0)WsI(T0) and the analogous liquid term.
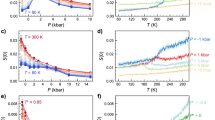
Figure 3a,b compare the theoretically predicted pm(T) to the coexistence pressure computed numerically by means of the interface-pinning method37. The density of the crystalline and liquid phases may also be computed by means of a first-order Taylor expansion working from the reference isomorph (see the ‘Methods’ section). Figure 3c compares the predicted (ρ,T) phase diagram based on equation (26) to that obtained by the interface-pinning MD simulations. Finally, Fig. 3d shows the predicted and simulated fusion entropy ΔSfus and enthalpy ΔHfus, the latter quantity being of course measured in experiments as the latent heat. In all cases there is good agreement between theoretical prediction and simulations.
The theoretical predictions are based on simulations at the coexistence reference state point indicated by an arrow in each figure (T0=2.0ɛ/kB), the MD simulations employed the interface-pinning method37, see the ‘Methods’ section. No fitting was done in these figures—the only input to the theory is properties of the coexisting liquid and crystal at the reference temperature. (a) Temperature–pressure phase diagram. The green dashed line marks the expectation based on a linear extrapolation of the Clausius–Clapeyron relation dpm/dT=ΔSfus/ΔVfus from the reference state point, that is, assuming that the entropy of fusion and the volume change are both constant. (b) The same data plotted with a linear pressure axis. (c) The freezing and melting lines in the density–temperature phase diagram; the coloured area is the coexistence region. (d) Fusion entropy (main panel) and enthalpy (inset).
Having in mind the fact that the pressure at the triple point is very low for the LJ system, we estimate the triple point temperature to Ttp=0.688(2)ɛ/kB from the theory by assuming zero pressure. This is within the statistical uncertainty of the triple point temperature computed with the interface-pinning method. For comparison, a linear extrapolation of the Clausius–Clapeyron relation from the reference temperature (the green dashed lines in Fig. 3a,b) predicts a triple point temperature of 0.909(2)ɛ/kB.
Since the melting line is not an isomorph, the Lindemann ratio is not invariant along it. The theory estimates the deviation from a constant Lindemann ratio by a first-order Taylor expansion from the reference isomorph (see Fig. 2 and the ‘Methods’ section). Figure 4a demonstrates good, though not perfect agreement between theory and numerical computations of the Lindemann ratio. The liquids’ self-diffusion constant plays an important role for the crystal growth rate as expressed, for example, in the Wilson–Frenkel law65,66. This motivated us to use the theory also for calculating the liquid’s diffusion constant variation along the freezing line (Fig. 4b). Another important component for crystal growth is the thermodynamic driving force on the crystal–liquid interface, which is the Gibbs free energy difference between the two phases, ΔG≅(Tm−T)ΔSfus (ΔSfus is shown on Fig. 3d). Finally, Fig. 4c shows the viscosity along the freezing line. In all cases the blue dashed lines mark the prediction if the dynamics were invariant in reduced units, that is, if the freezing/melting lines were isomorphs.
The blue dashed lines show the predictions if perfect invariance of structure and dynamics in reduced units applies along the freezing/melting lines, the arrows indicate the reference state point upon which the predictions are based. (a) Lindemann ratio along the melting line. (b) Self-diffusion constant along the freezing line. (c) Viscosity along the freezing line.
Discussion
The theory presented above predicts the thermodynamics of freezing and melting from a single coexistence state point. The theory also enables one to calculate the deviations from the invariance of several quantities along the melting line predicted by the hard-sphere melting picture22,16,30,31,32. The theory is analytic for LJ type systems, that is, systems involving a pair potential that is a difference of two inverse power laws, but the framework developed applies to any system with hidden scale invariance, including molecular systems. The theory works well for the LJ system, with the largest deviations found close to the triple point where the structure is less invariant along the reference isomorph (Fig. 1b).
Having established a firm foundation for the thermodynamics of freezing and melting for R simple systems, it is our hope that it will soon be possible to address the exciting questions of how nucleation and growth proceed, processes that are not well understood even for simple systems beyond the hard-sphere system67. It seems likely that variations of the nucleation and growth mechanisms along the melting line can be analyzed in the same way as above, that is, by utilizing the fact that the freezing and melting lines are close to isomorphs along which the dynamics is invariant to a quite good approximation.
It is not clear to which degree this approach to melting can be generalized to quantum systems for which an outstanding question is the possible existence of a zero-temperature quantum fluid of metallic hydrogen. The quantum nature of the proton modifies classical melting, for example by increasing the value of the Lindemann ratio68. It would be interesting to investigate whether melting of quantum crystals may be understood in the above framework, but this awaits the development of an isomorph theory for quantum systems. In ongoing work we are addressing another open question, namely whether the above can be generalized to deal with more realistic systems, for instance metals for which density-functional-theory computer simulations nowadays give realistic representations of the physics and have demonstrated hidden scale invariance for most metals49.
Methods
Computer simulations
We studied a LJ system of N=5,000 particles with pair interactions truncated and shifted at 6σ. Coexistence pressures, pm, are computed with the interface-pinning method37 in which coexistence state points are determined by computing the thermodynamic driving force on a solid-liquid interface. Table 1 lists the energy U0 and virial W0 at the reference temperature T0=2ɛ/kB for both the liquid and crystal states at coexistence. The A12 and A6 coefficients (for the liquid and the crystal separately) are computed from reference state-point data using equation (8) below. The derivatives of the A coefficients with respect to excess entropy,  and
and  , are computed from reference state-point data using equation (11) with the γ0's listed in Table 1. Melting pressures (Fig. 3a,b) are computed from reference state-point data using equation (21) in which the potential energies along the two reference isomorphs are expressed in equation (6). The densities along the liquid and crystal reference isomorphs are found as functions of temperature by inversion of equation (9) (upper equation). The second derivatives of the A coefficients,
, are computed from reference state-point data using equation (11) with the γ0's listed in Table 1. Melting pressures (Fig. 3a,b) are computed from reference state-point data using equation (21) in which the potential energies along the two reference isomorphs are expressed in equation (6). The densities along the liquid and crystal reference isomorphs are found as functions of temperature by inversion of equation (9) (upper equation). The second derivatives of the A coefficients,  and
and  , are given by equation (15) where the reference state point excess heat capacity and
, are given by equation (15) where the reference state point excess heat capacity and  are listed in Table 1. The freezing and melting densities (Fig. 3c) are computed from the pressures by combining equations (22) and (25). The entropy of fusion ΔSfus (Fig. 3d) is computed by combining equations (27, 28, 29, 30). The value of the Lindemann ratio L of the crystal at the reference temperature, L0 and its temperature derivative along an isochore, (∂L/∂T)ρ, are listed in Table 1. By letting X=L in equations (32) and (38), we arrive at the prediction shown in Fig. 4a. Similarly, the predictions of the self-diffusion constant D (Fig. 4b) and viscosity η (Fig. 4c) are found by letting
are listed in Table 1. The freezing and melting densities (Fig. 3c) are computed from the pressures by combining equations (22) and (25). The entropy of fusion ΔSfus (Fig. 3d) is computed by combining equations (27, 28, 29, 30). The value of the Lindemann ratio L of the crystal at the reference temperature, L0 and its temperature derivative along an isochore, (∂L/∂T)ρ, are listed in Table 1. By letting X=L in equations (32) and (38), we arrive at the prediction shown in Fig. 4a. Similarly, the predictions of the self-diffusion constant D (Fig. 4b) and viscosity η (Fig. 4c) are found by letting  and
and  , respectively. D is determined from the long-time limit of the mean-square displacement; η is computed using the SLLOD algorithm as detailed in ref. 27 except that in the present work we increased the number of particles to 4,096 and used the above-mentioned larger cutoff.
, respectively. D is determined from the long-time limit of the mean-square displacement; η is computed using the SLLOD algorithm as detailed in ref. 27 except that in the present work we increased the number of particles to 4,096 and used the above-mentioned larger cutoff.
We proceed to describe the theory in detail. The reference state point is selected at coexistence, that is, with known temperature T0 and pressure p0. There are two different reference densities, a solid and a liquid one, below denoted, respectively, by ρs,0 and by ρl,0. In the density–temperature phase diagram there are two reference isomorphs. The arguments developed in the next two sections refer to either one of these.
Isomorph characteristics of arbitrary R simple systems
As mentioned, the temperature–pressure reference state point defines two reference density–temperature state points, a liquid and a solid one. Let us focus on one of these with density ρ0 and temperature T0 (thus dropping in this and the next subsection subscripts s and l). From an NVT MD equilibrium simulation (for example, with a Nosé–Hoover thermostat) n configurations R10,R20,…,Rn0 are sampled. In order to map out the reference isomorph parametrized by density, one first identifies the temperature T such that (ρ,T) is on the isomorph through the reference state point (ρ0,T0). This is done as follows. If the configurations scaled uniformly to density ρ are denoted by R1,R2,…,Rn in which Ri=(ρ0/ρ)1/3Ri0, the temperature T is determined from the standard configurational temperature expression (in which the averages are over the n sampled configurations)

This determines the function  where we define the relative density along the isomorph by
where we define the relative density along the isomorph by  with superscript I indicating ‘isomorph’ (thus T(1)=T0). By averaging the potential energy U(R) and the virial W(R)≡(−1/3)R˙∇U(R) over the scaled configurations one identifies the functions
with superscript I indicating ‘isomorph’ (thus T(1)=T0). By averaging the potential energy U(R) and the virial W(R)≡(−1/3)R˙∇U(R) over the scaled configurations one identifies the functions  and
and  .
.  is found from the scaled configurations’ potential energy via CVex=〈(ΔU)2〉/kBT2 in which
is found from the scaled configurations’ potential energy via CVex=〈(ΔU)2〉/kBT2 in which  . The density-scaling exponent
. The density-scaling exponent  may be found either via the statistical-mechanical identity42,69 γ=〈ΔUΔW〉/〈(ΔU)2〉 or simply by taking the derivative of an analytical approximation to the the function
may be found either via the statistical-mechanical identity42,69 γ=〈ΔUΔW〉/〈(ΔU)2〉 or simply by taking the derivative of an analytical approximation to the the function  .
.
As shown in the below subsection ‘The melting-line pressure’, one now has enough information to calculate the pressure along the melting line, pm(T). To calculate the liquid and solid densities along the melting line (see subsection ‘The freezing- and melting-line densities’ below) one needs to know the below three partial derivatives. Denoting the derivative of the virial along the isomorph with respect to  by
by  and recalling that
and recalling that  and
and  (refs 42, 69), the three required quantities are given by
(refs 42, 69), the three required quantities are given by

The entropy of fusion ΔSfus is calculated by use of equations (27, 28, 29, 30) below. The three quantities needed here are given by

Isomorph characteristics of generalized LJ pair potentials
The above quantities may be calculated analytically for generalized LJ pair potentials, that is, for systems of particles interacting via pair potential(s) given as a sum or difference of two inverse power laws, r−m and r−n. The derivation given below applies for any exponents m>n>0 and for general multi-component systems; its subsequent application to freezing and melting deals with single-component systems only.
Invariance of the structure along an isomorph implies that the thermodynamic average potential energy at a given state point, U, may be written  (in this section the superscript I is dropped on the reference isomorph density) in which the two A coefficients are functions only of the excess entropy Sex. For simplicity of notation we shall not indicate the Sex dependence. The first and second order derivatives of Am with respect to Sex are marked by
(in this section the superscript I is dropped on the reference isomorph density) in which the two A coefficients are functions only of the excess entropy Sex. For simplicity of notation we shall not indicate the Sex dependence. The first and second order derivatives of Am with respect to Sex are marked by  and
and  and likewise for An.
and likewise for An.
The identity for the virial  implies
implies

At the reference state point  , so for determining Am and An from reference state-point data we have the following two equations:
, so for determining Am and An from reference state-point data we have the following two equations:

This implies

From the identity  and the definition of the density-scaling exponent,
and the definition of the density-scaling exponent,  , we get
, we get

For determining  and
and  from reference state-point data one has
from reference state-point data one has

This implies

In order to arrive at equations for  and
and  , we first note that
, we first note that  , that is,
, that is,  . This implies that
. This implies that  . If we define a thermodynamic quantity B by
. If we define a thermodynamic quantity B by

one has

The two equations for determining  and
and  from reference state-point data are thus
from reference state-point data are thus

This implies

In summary, we have shown that for each of the two reference isomorphs the six numbers Am, An,  ,
,  ,
,  and
and  may be found from reference state-point simulations determining: (1) the potential energy U0, (2) the virial W0, (3) the temperature T0, (4) the excess isochoric specific heat
may be found from reference state-point simulations determining: (1) the potential energy U0, (2) the virial W0, (3) the temperature T0, (4) the excess isochoric specific heat  , (5) the density-scaling exponent γ0 and (6) the derivative of CVex along the isomorph via the quantity B0 defined in equation (12). The first three quantities are determined directly. The next two quantities are determined from fluctuations at the reference state point:
, (5) the density-scaling exponent γ0 and (6) the derivative of CVex along the isomorph via the quantity B0 defined in equation (12). The first three quantities are determined directly. The next two quantities are determined from fluctuations at the reference state point:  and γ0=〈ΔWΔU〉/〈(ΔU)2〉. Finally, the quantity B0 is most accurately found from simulations along the reference isomorph carried out close to the reference state point, although in principle B0 can be calculated from fluctuations at the reference state point (those needed are of third order and consequently of considerable numerical uncertainty). We calculated B0 numerically by directly applying equation (12); alternatively, following the methods used in ref. 70 one may rewrite B as B=(γT/CVex)[1+(∂ ln γ/∂ ln T)ρ] and evaluate B0 from the (rather weak) constant-density temperature variation of γ at the reference state point.
and γ0=〈ΔWΔU〉/〈(ΔU)2〉. Finally, the quantity B0 is most accurately found from simulations along the reference isomorph carried out close to the reference state point, although in principle B0 can be calculated from fluctuations at the reference state point (those needed are of third order and consequently of considerable numerical uncertainty). We calculated B0 numerically by directly applying equation (12); alternatively, following the methods used in ref. 70 one may rewrite B as B=(γT/CVex)[1+(∂ ln γ/∂ ln T)ρ] and evaluate B0 from the (rather weak) constant-density temperature variation of γ at the reference state point.
The melting-line pressure
In the temperature–pressure phase diagram the freezing and melting lines are identical. This section shows how to calculate the pressure on this line as a function of temperature, pm(T), which is determined by equating the liquid and solid phase’s Gibbs free energies. Recalling that V=(∂G/∂p)T we estimate these from the Gibbs free energies along the isomorphs, GlI(T) and GsI(T), as follows (below FlI(T) is the Helmholtz free energy along the liquid reference isomorph and likewise for the solid)

The coexistence condition Gl(T,pm)=Gs(T,pm) leads to

If Fid is the ideal-gas Helmholtz free energy, the Helmholtz free energy along the liquid isomorph is given by

An analogous expression applies for the solid isomorph’s Helmholtz free energy,  , of course. The two constants
, of course. The two constants  and
and  are not known, but one needs only their difference. This is determined from the equilibrium condition at the reference state point, Gl(T0, p0)=Gs(T0, p0) as expressed in equation (17), leading, since pV=NkBT+W and Fid(T, ρl)−Fid(T, ρs)=NkBT ln(ρl/ρs), to
are not known, but one needs only their difference. This is determined from the equilibrium condition at the reference state point, Gl(T0, p0)=Gs(T0, p0) as expressed in equation (17), leading, since pV=NkBT+W and Fid(T, ρl)−Fid(T, ρs)=NkBT ln(ρl/ρs), to

The coexistence condition, equation (17), thus becomes (dropping the explicit temperature dependencies)

or, in terms of the relative density along the respective isomorphs  ,
,

In the case of an arbitrary potential there is no analytical expression for the (average) potential energy as a function of density. Here, the density (of each phase) is the control parameter and T is identified from equation (3), resulting by numerical inversion in two functions  and
and  . In the case of generalized LJ pair potentials, for a given temperature T the functions
. In the case of generalized LJ pair potentials, for a given temperature T the functions  and
and  are found by solving equation (9) (in general numerically, but analytically for the 12-6 LJ system), using the A′ coefficients of equation (11). The potential energy along the isomorphs is given by equation (6).
are found by solving equation (9) (in general numerically, but analytically for the 12-6 LJ system), using the A′ coefficients of equation (11). The potential energy along the isomorphs is given by equation (6).
The freezing- and melting-line densities
We work from the respective reference isomorphs knowing as functions of temperature the coexistence pressure, and the pressure along the reference isomorphs. From this information one calculates the solid and liquid densities by moving on an isotherm from the reference isomorph to the freezing/melting line (Fig. 2). In both cases we define the isothermal difference DW≡W(T)−WI(T). Here and thoughout the paper D refers to isothermal differences between the reference isomorph and the freezing/melting line.
At any given temperature T the density  of the liquid/solid at coexistence is calculated from
of the liquid/solid at coexistence is calculated from

If  is known, we can determine
is known, we can determine  from equation (22).
from equation (22).
The following standard identity is used

In the case of an arbitrary potential, the three terms on the right hand side are calculated from equation (4). For the generalized LJ case, these terms are expressed in terms of the A coefficients by making use of equations (6) and (9), resulting in

We thus have in the generalized LJ case

In both the arbitrary potential case and that of generalized LJ systems, the equation for the density ρ(T)=N/V(T) is found from equation (22) solved numerically in the form

The entropy of fusion
In this section we calculate the constant-pressure entropy of fusion ΔSfus. One way to do this is to use the Clausius–Clapeyron equation dpm/dT=ΔSfus/ΔVfus in which we now know all quantities except ΔSfus. An alternative method similar to the above proceeds as follows. Across the melting line one has ΔGfus=0, that is, ΔEfus−TΔSfus+pm(T)ΔVfus=0 (E is the total energy). Since the kinetic energy is the same for liquid and solid at the given temperature T, one has ΔEfus=ΔUfus and thus

This equation is used for evaluating ΔSfus from interface-pinning simulations. It is also used for predicting ΔSfus(T) by proceeding as follows. We have predictions for pm=pm(T) and for ΔVfus=Vl(T)−Vs(T). The missing term is ΔUfus=ΔUfus(T), which is estimated via

The partial derivatives refer to the respective reference isomorph as in the last section, and these are evaluated like those of W. Thus,

In the case of an arbitrary potential, the three terms on the right hand side are calculated from equation (5). For the generalized LJ case, these terms may be expressed in terms of the A coefficients of the reference isomorph as follows

We now have all information required for calculating the entropy of fusion.
Melting-line variation of isomorph invariants
We finally turn to the problem of evaluating how much an isomorph invariant X—in casu the reduced vibrational crystalline mean-square displacement, the reduced liquid-state diffusion constant, and the reduced liquid-state viscosity—varies along the freezing/melting line. The starting point is that

On the one hand

On the other hand we have the standard fluctuation formula

Combining these equations at the reference state point leads to (where subscript 0 denotes an equilibrium average at the reference state point)

Consider next an arbitrary temperature T on the freezing/melting line. If DSex is the difference between crystal (respectively) liquid excess entropy at melting and that of the corresponding reference isomorph at the same temperature and Dρ likewise is the difference between crystal (respectively) liquid density at melting and that of the corresponding reference isomorph, we estimate X via

Equation (4) implies

Thus we have

This implies

in which the partial derivative is evaluated at the reference state point. If X is a thermodynamic quantity, one may use the fluctuation expression, equation (34), to rewrite this as follows

This expression may be used in the case of an arbitrary potential, as well as for generalized LJ systems for which analytical expressions are available.
Data availability
The data presented in this study are available from the corresponding author upon request.
Additional information
How to cite this article: Pedersen, U.R. et al. Thermodynamics of freezing and melting. Nat. Commun. 7:12386 doi: 10.1038/ncomms12386 (2016).
References
Chandler, D. Introduction to Modern Statistical Mechanics Oxford University Press (1987).
Atkins, P. W. Physical Chemistry 4th edn (Oxford Univ. Press, 1990).
Glicksman, M. E. Principles of Solidification: An Introduction to Modern Casting and Crystal Growth Concepts Springer (2011).
Eggert, J. H. et al. Melting temperature of diamond at ultrahigh pressure. Nat. Phys. 6, 40–43 (2010).
Guillaume, C. L. et al. Cold melting and solid structures of dense lithium. Nat. Phys. 7, 211–214 (2011).
Peng Tan, N. X. & Xu, L. Visualizing kinetic pathways of homogeneous nucleation in colloidal crystallization. Nat. Phys. 10, 73–79 (2014).
Deutschländer, S., Puertas, A. M., Maret, G. & Keim, P. Specific heat in two-dimensional melting. Phys. Rev. Lett. 113, 127801 (2014).
Statt, A., Virnau, P. & Binder, K. Finite-size effects on liquid-solid phase coexistence and the estimation of crystal nucleation barriers. Phys. Rev. Lett. 114, 026101 (2015).
van der Waals, J. D. On the Continuity of the Gaseous and Liquid States. Ph.D. thesis, Universiteit Leiden (1873).
Lennard-Jones, J. E. On the determination of molecular fields. I. From the variation of the viscosity of a gas with temperature. Proc. R. Soc. Lond. A 106, 441–462 (1924).
Barker, J. A. & Henderson, D. What is ‘liquid’? Understanding the states of matter. Rev. Mod. Phys. 48, 587–671 (1976).
Gubbins, K., Smitha, W., Tham, M. & Tiepel, E. Perturbation theory for the radial distribution function. Mol. Phys. 22, 1089 (1971).
Hoover, W. G., Gray, S. G. & Johnson, K. W. Thermodynamic properties of the fluid and solid phases for inverse power potentials. J. Chem. Phys. 55, 1128–1136 (1971).
Weeks, J. D., Chandler, D. & Andersen, H. C. Role of repulsive forces in determining the equilibrium structure of simple liquids. J. Chem. Phys. 54, 5237–5247 (1971).
Hausleitner, C., Kahl, G. & Hafner, J. Liquid structure of transition metals: investigations using molecular dynamics and perturbation- and integral-equation techniques. J. Phys.: Condens. Mat 3, 1589 (1991).
Hansen, J.-P. & McDonald, I. R. Theory of Simple Liquids: With Applications to Soft Matter 4th edn (Academic, 2013).
Hansen, J.-P. & Verlet, L. Phase transitions of the Lennard-Jones system. Phys. Rev. 184, 151–161 (1969).
Rosenfeld, Y. Theory of simple classical fluids: universality in the short-range structure. Phys. Rev. A 20, 1208–1235 (1979).
Waseda, Y., Yokoyama, K. & Suzuki, K. Structure of molten Mg, Ca, Sr, and Ba by X-ray diffraction. Z. Naturforsch. A 30, 801–805 (1975).
Ross, M. Generalized Lindemann melting law. Phys. Rev. 184, 233–242 (1969).
Lindemann, F. A. Über die Berechning molekularer Eigenfrequenzen. Phys. Z. 11, 609 (1910).
Lawson, A. C. An improved Lindemann melting rule. Philos. Mag. B 81, 255–266 (2001).
Stishov, S. M. The thermodynamics of melting of simple substances. Sov. Phys. Usp. 17, 625–643 (1975).
Luo, S.-N., Strachan, A. & Swift, D. C. Vibrational density of states and Lindemann melting law. J. Chem. Phys. 122, 194709 (2005).
Chakravarty, C., Debenedetti, P. G. & Stillinger, F. H. Lindemann measures for the solid–liquid phase transition. J. Chem. Phys. 126, 204508 (2007).
Andrade., E. N. C. A theory of the viscosity of liquids—Part I. Phil. Mag. 17, 497–511 (1934).
Costigliola, L., Schrøder, T. B. & Dyre, J. C. Freezing and melting line invariants of the Lennard-Jones system. Phys. Chem. Chem. Phys. 18, 14678–14690 (2016).
Hansen, J.-P. Phase transition of the Lennard-Jones system. II. High-temperature limit. Phys. Rev. A 2, 221–230 (1970).
Tallon, J. L. The entropy change on melting of simple substances. Phys. Lett. A 76, 139–142 (1980).
Pedersen, U. R., Hummel, F. & Dellago, C. Computing the crystal growth rate by the interface pinning method. J. Chem. Phys. 142, 044104 (2015).
Benjamin, R. & Horbach, J. Crystal growth kinetics in Lennard-Jones and Weeks–Chandler–Andersen systems along the solid–liquid coexistence line. J. Chem. Phys. 143, 014702 (2015).
Heyes, D. M. & Branka, A. C. The Lennard-Jones melting line and isomorphism. J. Chem. Phys. 143, 234504 (2015).
Agrawal, R. & Kofke, D. A. Solid–fluid coexistence for inverse-power potentials. Phys. Rev. Lett. 74, 122 (1995).
Ben-Amotz, D. & Stell, G. Hard sphere perturbation theory for fluids with soft-repulsive-core potentials. J. Chem. Phys. 120, 4844 (2004).
Heyes, D. M., Dini, D. & Branka, A. C. Scaling of Lennard-Jones liquid elastic moduli, viscoelasticity and other properties along fluid–solid coexistence. Phys. Status Solidi (b) 252, 1514–1525 (2015).
Ding, Y. & Mittal, J. Equilibrium and nonequilibrium dynamics of soft sphere fluids. Soft Matter 11, 5274–5281 (2015).
Pedersen, U. R. Direct calculation of the solid–liquid Gibbs free energy difference in a single equilibrium simulation. J. Chem. Phys. 139, 104102 (2013).
Dyre, J. C. Hidden scale invariance in condensed matter. J. Phys. Chem. B 118, 10007–10024 (2014).
Schrøder, T. B. & Dyre, J. C. Simplicity of condensed matter at its core: generic definition of a Roskilde-simple system. J. Chem. Phys. 141, 204502 (2014).
Pedersen, U. R., Bailey, N. P., Schrøder, T. B. & Dyre, J. C. Strong pressure–energy correlations in van der Waals liquids. Phys. Rev. Lett. 100, 015701 (2008).
Bailey, N. P., Pedersen, U. R., Gnan, N., Schrøder, T. B. & Dyre, J. C. Pressure-energy correlations in liquids. I. Results from computer simulations. J. Chem. Phys. 129, 184507 (2008).
Gnan, N., Schrøder, T. B., Pedersen, U. R., Bailey, N. P. & Dyre, J. C. Pressure-energy correlations in liquids. IV. Isomorphs in liquid phase diagrams. J. Chem. Phys. 131, 234504 (2009).
Maimbourg, T. & Kurchan, T. Approximate scale invariance in particle systems: a large-dimensional justification EPL 114, 60002 (2016).
Roland, C. M., Hensel-Bielowka, S., Paluch, M. & Casalini, R. Supercooled dynamics of glass-forming liquids and polymers under hydrostatic pressure. Rep. Prog. Phys. 68, 1405–1478 (2005).
Gundermann, D. et al. Predicting the density-scaling exponent of a glass-forming liquid from prigogine-defay ratio measurements. Nat. Phys. 7, 816–821 (2011).
Xiao, W., Tofteskov, J., Christensen, T. V., Dyre, J. C. & Niss, K. Isomorph theory prediction for the dielectric loss variation along an isochrone. J. Non-Cryst. Solids 407, 190–195 (2015).
Pedersen, U. R., Schrøder, T. B. & Dyre, J. C. Repulsive reference potential reproducing the dynamics of a liquid with attractions. Phys. Rev. Lett. 105, 157801 (2010).
Ingebrigtsen, T. S., Errington, J. R., Truskett, T. M. & Dyre, J. C. Predicting how nanoconfinement changes the relaxation time of a supercooled liquid. Phys. Rev. Lett. 111, 235901 (2013).
Hummel, F., Kresse, G., Dyre, J. C. & Pedersen, U. R. Hidden scale invariance of metals. Phys. Rev. B 92, 174116 (2015).
Malins, A., Eggers, J. & Royall, C. P. Investigating isomorphs with the topological cluster classification. J. Chem. Phys 139, 234505 (2013).
Abramson, E. H. Viscosity of fluid nitrogen to pressures of 10 GPa. J. Phys. Chem. B 118, 11792–11796 (2014).
Fernandez, J. & Lopez, E. R. Experimental Thermodynamics: Advances in Transport Properties of Fluids ch. 9.3, 307–317 (Royal Society of Chemistry, 2014).
Flenner, E., Staley, H. & Szamel, G. Universal features of dynamic heterogeneity in supercooled liquids. Phys. Rev. Lett. 112, 097801 (2014).
Prasad, S. & Chakravarty, C. Onset of simple liquid behaviour in modified water models. J. Chem. Phys. 140, 164501 (2014).
Buchenau, U. Thermodynamics and dynamics of the inherent states at the glass transition. J. Non-Cryst. Solids 407, 179–183 (2015).
Grzybowska, K., Grzybowski, A., Pawlus, S., Pionteck, J. & Paluch, M. Role of entropy in the thermodynamic evolution of the time scale of molecular dynamics near the glass transition. Phys. Rev. E 91, 062305 (2015).
Harris, K. R. & Kanakubo, M. Self-diffusion, velocity cross-correlation, distinct diffusion and resistance coefficients of the ionic liquid [BMIM][Tf2N] at high pressure. Phys. Chem. Chem. Phys. 17, 23977–23993 (2015).
Ingebrigtsen, T. S. & Tanaka, H. Effect of size polydispersity on the nature of Lennard-Jones liquids. J. Phys. Chem. B 119, 11052–11062 (2015).
Kipnusu, W. K. et al. Confinement for more space: a larger free volume and enhanced glassy dynamics of 2-ethyl-1-hexanol in nanopores. J. Phys. Chem. Lett. 6, 3708–3712 (2015).
Schmelzer, J. W. P. & Tropin, T. V. Kinetic criteria of glass-formation, pressure dependence of the glass-transition temperature, and the PrigogineDefay ratio. J. Non-Cryst. Solids 407, 170–178 (2015).
Khrapak, S. A., Klumov, B., Couedel, L. & Thomas, H. M. On the long-waves dispersion in Yukawa systems. Phys. Plasmas 23, 023702 (2016).
Adrjanowicz, K., Paluch, M. & Pionteck, J. Isochronal superposition and density scaling of the intermolecular dynamics in glass-forming liquids with varying hydrogen bonding propensity. RSC Adv. 6, 49370 (2016).
Powles, J. G., Rickayzen, G. & Heyes, D. M. Temperatures: old, new and middle aged. Mol. Phys. 103, 1361–1373 (2005).
Rosenfeld, Y. New method for equation-of-state calculations: linear combinations of basis potentials. Phys. Rev. A 26, 3633–3645 (1982).
Wilson, H. A. On the velocity of solidification and viscosity of supercooled liquids. Philos. Mag. 50, 238–250 (1900).
Frenkel, J. Kinetic Theory of Liquids Clarendon (1946).
Auer, S. & Frenkel, D. Prediction of absolute crystal-nucleation rate in hard-sphere colloids. Nature 409, 1021–1023 (2001).
Chui, S. T. Solidification instability of quantum fluids. Phys. Rev. B 41, 796–798 (1990).
Bailey, N. P., Pedersen, U. R., Gnan, N., Schrøder, T. B. & Dyre, J. C. Pressure–energy correlations in liquids. II. Analysis and consequences. J. Chem. Phys. 129, 184508 (2008).
Bailey, N. P., Bøhling, L., Veldhorst, A. A., Schrøder, T. B. & Dyre, J. C. Statistical mechanics of Roskilde liquids: configurational adiabats, specific heat contours, and density dependence of the scaling exponent. J. Chem. Phys. 139, 184506 (2013).
Acknowledgements
We are indebted to Karolina Adrjanowicz and Kristine Niss for inspiring the present work via their attempts at interpreting crystallization data for van der Waals liquids in terms of the isomorph theory. This work was supported by the Villum Foundation by the YIP Grant VKR-023455 and by the Danish National Research Foundation by Grant DNRF61.
Author information
Authors and Affiliations
Contributions
The project was conceived by U.R.P. and N.P.B. Computations were carried out by U.R.P. and L.C. The theory was devised by J.C.D. based on initial works by N.P.B. and T.B.S. The paper was written by U.R.P. and J.C.D.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Pedersen, U., Costigliola, L., Bailey, N. et al. Thermodynamics of freezing and melting. Nat Commun 7, 12386 (2016). https://doi.org/10.1038/ncomms12386
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms12386
This article is cited by
-
Evidence of a one-dimensional thermodynamic phase diagram for simple glass-formers
Nature Communications (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.