Abstract
Topological insulators interacting with magnetic impurities have been reported to host several unconventional effects. These phenomena are described within the framework of gapping Dirac quasiparticles due to broken time-reversal symmetry. However, the overwhelming majority of studies demonstrate the presence of a finite density of states near the Dirac point even once topological insulators become magnetic. Here, we map the response of topological states to magnetic impurities at the atomic scale. We demonstrate that magnetic order and gapless states can coexist. We show how this is the result of the delicate balance between two opposite trends, that is, gap opening and emergence of a Dirac node impurity band, both induced by the magnetic dopants. Our results evidence a more intricate and rich scenario with respect to the once generally assumed, showing how different electronic and magnetic states may be generated and controlled in this fascinating class of materials.
Similar content being viewed by others
Introduction
Topological insulators (TIs) represent a new state of matter where electronic properties are not related to any symmetry breaking but dictated by the concept of topology. Beyond their fundamental interest, the separation of electronic states into a gapped bulk and a helical spin Dirac cone at the surface offers great potential for applications. Ultimately, the success of TIs crucially depends on the ability of functionalizing them with well-defined perturbations. Within this framework, magnetic dopants occupy a primary role1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18. As they break the time-reversal symmetry that protects topological states, they are expected to modify the Dirac spectrum while at the same time changing the spin-texture5,6,7,8. This interaction is expected to result in several exotic phenomena with interesting implications in spintronics and magneto-electric applications1,2,3,4. The recent experimental realization of the quantum anomalous Hall effect confirmed the presence of a gapped Dirac state3,4. On the other hand, the majority of photoemission9,10,11,12,13 and local tunnelling data14,15,16,17,18 clearly demonstrate the presence of a finite density of states (DOS) near the Dirac node in magnetically doped TIs. The disorder induced by the dopants further complicates the story as it generates spatial fluctuations of the chemical potential16, which significantly broaden the lineshape of photoemission spectra potentially impeding the detection of a gap9,10,11,12,13. Recent theoretical predictions suggested that the resolution of this apparent paradox might be directly linked to the dual nature of the electronic states generated by magnetic impurities19. However, these claims escaped experimental verification.
In the following, we provide compelling evidence that on one hand the emergence of ferromagnetism gaps the Dirac states and on the other hand impurity-induced resonances form an impurity band at or near the Dirac node filling the gap. Both effects originate from the same magnetic impurity doping, leading to the emergence of a two-fluid behaviour. Our results resolve long-standing contradictions in the field. They paint a more complicated and multifaceted story of magnetically doped TIs and provide a detailed microscopic picture that allows engineering electronic and magnetic properties by acting on the delicate balance in between the impurity band and the gapped Dirac states.
Results
Structural and magnetic properties
Figure 1a shows a photographic image representative of the bulk single crystals used in the present study, that is, vanadium (V)-doped Sb2Te3. This system recently led to the robust experimental realization of the quantum anomalous Hall effect4, thus being an optimal platform to investigate the interaction of topological states with time-reversal symmetry breaking perturbation. The nominal stoichiometry corresponds to Sb1.985V0.015Te3. Consequently, within the typical quintuple-layered structure characterizing these materials, V atoms substitute Sb as sketched in Fig. 1b at a concentration of 0.75% in each Sb plane. Figure 1c shows a typical large-scale topographic image of the samples acquired by scanning tunnelling microscopy (STM) in the constant-current mode. Dark points correspond to V atoms. Their introduction results in the creation of local perturbations in the crystal structure, which are imaged as depressions at the surface. Note that the V atoms are homogeneously distributed over the surface, without any clustering. This observation proves the good quality of the crystals used in our experiments, which can thus be classified as diluted doped. A quantitative estimation of the V concentration can be achieved by counting the number of depression visible on the surface, giving a value of 0.725% in each Sb layer, in good agreement with the nominal concentration of the crystals. Figure 1d shows an atomically resolved image of the area highlighted by a black box in Fig. 1c. This zoomed image allows visualizing two different V species marked by arrows. An analysis of their appearance based on their symmetry and surface extension allows, as described in ref. 20, to identify them as V atoms located in the second (A) and fourth Sb (B) atomic layer, respectively.
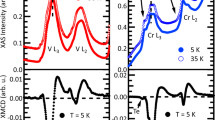
(a) Vanadium bulk-doped Sb2Te3 single crystal (Sb1.985V0.015Te3); (b) Sb2Te3 crystal structure: V atoms (green) are located in the second and fourth layer, substituting Sb; (c) 75 × 75 nm2 topographic image showing the absence of any clustering; (d) high-resolution image showing the V substitutional sites. Triangular depressions labelled as A and B correspond to the two possible V substitutional sites located in the second and fourth layer, respectively; (e) schematic of XMCD measurements. Photons with well-defined circular polarization and energy are absorbed by the sample in a variable magnetic field. The resulting photocurrent (total electron yield (TEY)) is measured, making the technique sensitive to surface magnetism. (f) TEY signals for opposite magnetic fields (blue and red lines) of B=±1 T. Their difference (green line) sheds light on the magnetic response of the V dopants; (g) out-of-plane V-L3 XMCD magnetization curve: the square shape of the hysteresis loop proves the existence of long-range surface ferromagnetic order.
To investigate the magnetic response of the TI to the introduction of magnetic dopants, X-ray magnetic circular dichroism (XMCD) measurements have been performed at the PM3 bending magnet beamline of Helmholtz-Zentrum Berlin HZB21 with a custom XMCD end station. X-ray absorption was recorded in the total electron yield mode in the presence of an external magnetic field, by measuring the photoinduced sample drain current, as schematically illustrated in Fig. 1e. The short probing depth of this technique22 allows investigating the existence of magnetic order at the surface, that is, where the topologically protected states exist. Figure 1f reports X-ray absorption spectra taken at the V L2,3 edges at a temperature of T=13.2 K in a magnetic field of ±1 T applied along the surface normal. Their difference (=XMCD; green line) highlights the considerable magnetic polarization of the near-surface V dopants and hence the existence of uncompensated magnetic moments. An XMCD hysteresis curve acquired at the same temperature is reported in Fig. 1g. Its square shape proves the ferromagnetic nature of this polarization and a high degree of homogeneity (absence of domain wall pinning), whereas the full remanence characterizes the surface normal as the easy direction of magnetic anisotropy.
Impact of impurities on topological states and emergence of Dirac node excitations
To visualize the impact of impurity ferromagnetism on the topological states, STS measurements have been performed on the very same crystals at T=4.8 K, that is, well below the Curie temperature. The local density of states (LDOS) for energies centred around the Dirac point, that is, where a gap is expected to open, is reported in Fig. 2a by positioning the tip away from any defects. The steep increase of the conductance visible at ∼50 and 200 meV above the Fermi level corresponds to the onset of the valence (VB) and conduction band (CB), respectively. Within this energy range, the conductance is strongly suppressed because of the bulk gap20. Spectroscopic measurements optimized over this energy range reveal that, although strongly reduced, the conductance never goes to zero but simply reaches a minimum at ∼175 meV. Unlike in the pristine scenario, where a pure V-shape characterizes STS spectra inside the bulk-gap20,23, this minimum is energetically close to but not directly at the Dirac point (see below). These data unequivocally demonstrate that, contrary to what is generally assumed, a spectral gap does not open at the Dirac point despite the presence of long-range surface magnetic order, which breaks the time-reversal symmetry protecting topological states.
(a) Scanning tunnelling spectroscopy of the ferromagnetic Sb1.985V0.015Te3. Data have been acquired by positioning the tip away from any defect. The density of states reaches a minimum (see arrow) at ∼175 meV above the Fermi level. The spectra reveal the absence of any gap opening despite the existence of long-range ferromagnetic order (see zoomed area). Stabilization parameters: I=50 pA, V=450 mV, zoomed area I=50 pA, V=225 mV; (b,c) spectroscopic measurements taken along lines crossing the two different V sites (see insets). In both cases, strong resonances energetically located close to the Dirac point (indicated by BS) emerge in the nearby of the dopants; (d,e) spatial dependence of the dopants induced resonances for b,c, respectively. The zero in the distance axis corresponds to the position of maximum intensity. In both cases, the spectral weight decays over distances of few nanometres. T=4.8 K.
To shed light on the origin of the finite LDOS, STS measurements have been performed by positioning the tip on top of the V dopants. This allows to directly investigate the V-induced modification of the site-specific electronic properties of the system. In both cases, that is, V atoms occupying the second and fourth layer (Fig. 2b,c, respectively), STS spectra visualize the emergence of strong resonances energetically located close to the Dirac point24. Figure 2d,e maps the spatial distribution of their intensity, revealing that their spectral weight is spread over distances of few nanometres, that is, the same length scale as the average distance between dopants (Fig. 1c). These impurity-induced resonances are thus significantly overlapping and likely form an impurity band centred at the resonance energy with a non-negligible spectral weight over the entire surface. Note that the energy position of these resonances is always in close proximity of the Dirac point, that is, where a gap is expected to open because of the magnetically ordered state.
In the following, we demonstrate that their experimental detection is consistent with the expected universal response to perturbations of Dirac materials25, that is, materials such as d-wave superconductors, graphene and, like in the present case, TIs, whose low-energy excitation spectra is described by massless Dirac particles rather than the Schrödinger equation. This implies that the behaviour of topological states with respect to time-reversal symmetry breaking cannot always be correctly described within the generally assumed framework of gapless versus magnetically gapped states, but that it reflects the competition between the trends for gapping due to magnetic scattering and gap filling due to impurity resonances filling up the gap6,7,19.
Dual nature of magnetic dopants: theory discussion
Once local impurities with both magnetic (JS) and scalar potential (U) scattering components are introduced in the system6,7,24,25, the Hamiltonian can be expressed as:

Here, J and U are the impurity magnetic exchange and potential strengths, respectively, whereas k is the wave vector. n(ri) and σ(ri) are the electronic number and spin densities, respectively, at the location, ri,, of the ith impurity. We have chosen units such that the Planck’s constant, ħ, and the Fermi (Dirac) velocity, vD, are both unity.
When the impurities align ferromagnetically perpendicular to the surface (z-direction), it is usually assumed that an energy gap appears at the Dirac point as a result of the spatially averaged carrier–impurity exchange interaction. However, this analysis ignores the role of the impurity potential strength, U, which leads to intragap resonances6,7,19. Taking this contribution into account, the effective Hamiltonian, including a mean-field gap arising from the magnetic moments, becomes

The mass,

is half the energy gap of the now massive surface Dirac states, found from an averaging procedure over the impurity-carrier exchange interactions, and Jeff is the residual effective magnetic impurity strength of the impurity acting on these massive Dirac fermions. Calculating the exact Green’s function of this effective Hamiltonian with the T-matrix method6 in the presence of a single impurity, we find analytically that when the scalar potential strength, U, is larger in magnitude than the residual exchange, JeffS, bound states appear inside the magnetization-induced energy gap. Bound states fill up the spectral gap as shown in Fig. 3. This finding demonstrates that our theoretical approach correctly captures the experimental data (Fig. 2a–e). For a more detailed discussion, see Supplementary Note 1 and Supplementary Figures 1 and 2.
(a) Theoretically calculated LDOS at a location with many nearby impurities, using the mean field theory, equation (2). In units where ħ, the Fermi velocity and the gap parameter, Δ, are unity, we have used the impurity strength parameters JeffS=0.5, U=1.75, high energy cutoff Λ=50, and the energy broadening parameter Γ=0.3. Impurities are located at distances r=0.6, 1.4, 1.5, 1.6, 1.8, 1 and 3 to mimic their experimental distribution. We have ignored multi-impurity scattering, which would lead to further broadening of the bound state feature (indicated as BS). The dashed curve is the LDOS in the absence of local impurity perturbation. As illustrated in (b) for negligible energy broadening (Γ=0.01), a clear magnetization-induced energy gap exists between ±Δ. When the absolute value of  is larger than a threshold (equal to 1 for Γ=0), bound states appear inside the gap. Thus, experimental measurements of the LDOS may never show a spectral gap, even though the mobility (transport) gap is nonzero because the localized intra-gap bound states do not affect long range transport at low temperatures.
is larger than a threshold (equal to 1 for Γ=0), bound states appear inside the gap. Thus, experimental measurements of the LDOS may never show a spectral gap, even though the mobility (transport) gap is nonzero because the localized intra-gap bound states do not affect long range transport at low temperatures.
These results paint a more intricate and rich scenario than the general assumption of a spectral gap appearing in magnetic TIs. In particular, they demonstrate the emergence of a two-fluid behaviour induced by the magnetic dopants, which drive a competition in between two different and opposite trends: gap opening versus gap filling which, as in the present case, can coexist.
Two-fluid behaviour and mobility gap
This behaviour might sound counterintuitive or even in conflict with the observation of phenomena such as the quantum anomalous Hall effect within this class of systems. In the following, we demonstrate that this is not the case, and that this apparent discrepancy reflects the localized versus delocalized nature of the impurity induced states, and their different response to electric and magnetic fields. This can be directly visualized by performing Landau level (LL) spectroscopy at high magnetic fields. Figure 4a–d reports the results obtained on pristine Sb2Te3. For sufficiently strong magnetic fields applied perpendicular to the surface, a sequence of peaks starts to emerge from the background, signalling the condensation of the two-dimensional topological states into a well-defined sequence of LLs26. As expected for linearly dispersing states27, all LLs can be nicely fitted by the relation:
Landau levels measured by scanning tunnelling spectroscopy in high magnetic fields on a pristine (a–d) and (e–h) V-doped Sb2Te3. The spectrum obtained at zero-field has been subtracted in both cases. Spectra at different magnetic fields have been vertically shifted for clarity. The number n identifies the Landau level index. Although all Landau levels of pristine Sb2Te3 can nicely be fit linearly, this is not the case for Sb1.985V0.015Te3. In this case, the onset of ferromagnetism shifts the zero Landau level towards higher energies, signalling the mass acquisition of the helical Dirac fermions. (g) The creation of a mobility gap despite the existence of a finite density of states generated by the magnetic impurities (grey shadow) is illustrated. As schematically illustrated in h, these states are filling the gap opened by the broken time-reversal symmetry. Their existence is intimately linked to the dual nature of the dopants, which result in the emergence of a two-fluid behaviour with opposite and competing trends.

where n is the LL index, B the magnetic field and vD the Dirac velocity, which describes the LLs energy sequence for massless particles.
Remarkably, once the same measurements are performed on the magnetically ordered V-doped samples (Fig. 4e–h), the zero-order LL does not follow the fit, but shifts towards higher energies. This is highlighted by the substantial shift of the first peak visible in Fig. 4e with respect to the dashed grey line, which marks the position of the zero-order LL as expected for linearly dispersing Dirac states (raw STS data before zero-field background subtraction are reported in Supplementary Fig. 3). This behaviour unambiguously signals the emergence of a mobility edge for the topological states. The emergence of mobility edges is well-documented in two-dimensional conventional quantum Hall states28. In TIs, the evolution of the LLs for Dirac states, mixed with a continuum of localized states, has the dispersion

Here, with respect to the pristine case, the appearance of Δ signals the acquisition of a mass term for the Dirac states. As shown in Fig. 4f, this equation describes the experimental data very well, the main effect of the mass term being manifested in a shift of the zero-order LL. Concurrently, the magnetic dopants also produce a continuum of localized states as indicated by the shaded regions in Fig. 4g,h. These states also fill the spectral gap about the Dirac point. In agreement with our theoretical arguments, we have found that these are mainly localized states bound to magnetic dopants (Fig. 2d,e). Consequently, once the chemical potential is tuned to their energy range, a mobility gap appears, enabling a full anomalous quantum Hall effect quantization while at the same time inducing a finite DOS at all energies.
Discussion
In conclusion, we demonstrated that magnetic dopants induce multiple changes with opposite trends in the excitation spectra of TIs. Contrary to what is generally believed, this competition may give rise to the coexistence of long-range magnetic order and gapless states. The microscopic origin of this behaviour is directly linked to the dual nature of the dopants, which on one hand induce a mass term in the Dirac spectrum, whereas at the same time create intragap states with large spectral density within the magnetic gap. Overall, this delicate balance results in the emergence of a two fluid behaviour where the localization of the impurity resonances produces a mobility gap. Our observations call for a reevaluation of the claims about magnetically doped TI. More generally, they provide evidence of the richness of the physics of TIs demonstrating how, going beyond a single-particle approach, it is possible to tailor the competition between opposite trends paving the way to engineer novel spintronics and magneto-electric effects in this fascinating class of materials.
Methods
Crystal growth
Single crystals of ∼10 mm in diameter and 60 mm in length were grown by the modified vertical Bridgman method with rotating heat field29. Required stoichiometric amounts of Sb, V and Te were loaded to a carbon-coated quartz ampoule. After evacuation to p=10−4 Torr the ampoule translation rate and axial temperature gradient were set to 10 mm per day and 15 °C cm−1, respectively.
STM measurements
Single crystals have been cleaved at room temperature in ultra-high-vacuum and immediately inserted into the STM operated at cryogenic temperatures. All measurements have been performed using electrochemically etched tungsten tips. Spectroscopic data have been obtained using the lock-in technique by adding a bias voltage modulation in between 1 and 10 meV (r.m.s.) at a frequency of f=793 Hz. Data displayed in Figs 1 and 2 have been obtained using a commercial STM operated at T=4.8 K. LL spectroscopy data (Fig. 4) have been obtained using a home-built STM operated at T=1.3 K. The exact energy position of the LLs has been obtained by considering the maximum of a gaussian function fitting each peak after background subtraction.
Data availability
The authors declare that the data supporting the findings of this study are available within the article and its Supplementary Information. Data files are available from the corresponding author upon request.
Additional information
How to cite this article: Sessi, P. et al. Dual nature of magnetic dopants and competing trends in topological insulators. Nat. Commun. 7:12027 doi: 10.1038/ncomms12027 (2016).
References
Qi, X.-L., Li, R., Zang, J. & Zhang, S.-C. Inducing a magnetic monopole with topological surface states. Science 232, 1184–1187 (2009).
Garate, I. & Franz, M. Inverse spin-galvanic effect in the interface between a topological insulator and a ferromagnet. Phys. Rev. Lett. 104, 146802 (2010).
Chang, C.-Z. et al. Experimental observation of the quantum anomalous hall effect in a magnetic topological insulator. Science 340, 167–170 (2013).
Chang, C.-Z. et al. High-precision realization of robust quantum anomalous hall state in a hard ferromagnetic topological insulator. Nat. Mater 14, 473–477 (2015).
Liu, Q., Liu, C.-X., Xu, C., Qi, X.-L. & Zhang, S.-C. Magnetic impurities on the surface of a topological insulator. Phys. Rev. Lett. 102, 156603 (2009).
Biswas, R. R. & Balatsky, A. V. Impurity-induced states on the surface of three-dimensional topological insulators. Phys. Rev. B 81, 233405 (2010).
Black-Schaffer, A. M. & Balatsky, A. V. Strong potential impurities on the surface of a topological insulator. Phys. Rev. B 85, 121103(R) (2012).
Zhu, J.-J., Yao, D.-X., Zhang, S.-C. & Chang, K. Electrically controllable surface magnetism on the surface of topological insulators. Phys. Rev. Lett. 106, 097201 (2011).
Chen, Y. L. et al. Massive dirac fermion on the surface of a magnetically doped topological insulator. Science 329, 659–662 (2010).
Xu, S.-Y. et al. Hedgehog spin texture and berry’s phase tuning in a magnetic topological insulator. Nat. Phys 8, 616–622 (2012).
Valla, T., Pan, Z.-H., Gardner, D., Lee, Y. S. & Chu, S. Photoemission spectroscopy of magnetic and nonmagnetic impurities on the surface of the Bi2Se3 topological insulator. Phys. Rev. Lett. 108, 117601 (2012).
Scholz, M. R. et al. Tolerance of topological states towards magnetic moments: Fe on Bi2Se3 . Phys. Rev. Lett. 108, 256810 (2012).
Schlenk, T. et al. Controllable magnetic doping of the surface state of a topological insulator. Phys. Rev. Lett. 110, 126804 (2013).
Hor, Y. S. et al. Development of ferromagnetism in the doped topological insulator Bi2− xMnxTe3 . Phys. Rev. B 81, 195203 (2010).
Okada, Y. et al. Direct observation of broken time-reversal symmetry on the surface of a magnetically doped topological insulator. Phys. Rev. Lett. 106, 206805 (2011).
Beidenkopf, H. et al. Spatial fluctuations of helical dirac fermions on the surface of topological insulators. Nat. Phys 7, 939–943 (2011).
Yang, F. et al. Identifying magnetic anisotropy of the topological surface state of Cr0.05Sb1.95Te3 with spin polarized STM. Phys. Rev. Lett. 111, 176802 (2013).
Sessi, P. et al. Signatures of dirac fermion mediated magnetic order. Nat. Comm 5, 5349 (2014).
Black-Schaffer, A. M., Balatsky, A. V. & Fransson, J. Filling of magnetic –impurity-induced gap in topological insulators by potential scattering. Phys. Rev. B 91, 201411 (R) (2015).
Jiang, Y. et al. Fermi-level tuning of epitaxial Sb2Te3 thin films on graphene by regulating intrinsic defects and substrate transfer doping. Phys. Rev. Lett. 108, 066809 (2012).
Kachel, T., Eggenstein, F. & Follath, R. A soft x-ray plane-grating monochromator optimized for elliptical dipole radiation from modern sources. J. Synchrotron Rad 22, 1301–1305 (2015).
Gambardella, P. et al. Ferromagnetism in one-dimensional monoatomic metal chains. Nature 416, 301–304 (2002).
Sessi, P. et al. Scattering properties of the three-dimensional topological insulator Sb2Te3: coexistence of topologically trivial and nontrivial surface states with opposite spin-momentum helicity. Phys. Rev. B 93, 035110 (2016).
Alpichshev, Z. et al. STM imaging of impurity resonances on Bi2Se3 . Phys. Rev. Lett. 108, 206402 (2012).
Wehling, T. O., Black-Schaffer, A. M. & Balatsky, A. V. Dirac materials. Adv. Phys 63, 1–76 (2014).
Jiang, Y. et al. Landau quantization and the thickness limit of topological insulator thin films of Sb2Te3 . Phys. Rev. Lett. 108, 016401 (2012).
Miller, D. L. et al. Observing the quantization of zero mass carriers in graphene. Science 324, 924–927 (2009).
Das Sarma, S. & Pinczuk, A. Perspectives in Quantum Hall Effects Wiley-VCH (2004).
Kokh, K. A., Makarenko, S. V., Golyashov, V. A., Shegai, O. A. & Tereshchenko, O. E. Melt growth of bulk Bi2Te3 crystals with a natural p–n junction. CrystEngComm 16, 581–584 (2014).
Acknowledgements
Work was supported by the US DOE E304, VR and KAW (A.V.B.) and by DFG through SFB 1170 ‘ToCoTronics’, project A02 (P.S., T.B., O.S., S.W., M.B.). R.R.B. thanks Purdue University Startup funds for support. Allocation of synchrotron radiation beamtime as well as financial support by HZB is gratefully acknowledged. We are grateful to A. Black-Schaffer, J. Fransson and T. Wehling for useful discussions.
Author information
Authors and Affiliations
Contributions
P.S., T.B., O.S. and S.W. performed and analysed STM and STS measurements. T.B., A.B. and K.F. performed XMCD measurements, K.F. analysed them. K.A.K. and O.E.T. synthesized the crystals. R.R.B. and A.V.B. provided the theoretical framework. All authors discussed the results and contributed in writing the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-3, Supplementary Note 1 and Supplementary References (PDF 404 kb)
Peer Review file
(PDF 232 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Sessi, P., Biswas, R., Bathon, T. et al. Dual nature of magnetic dopants and competing trends in topological insulators. Nat Commun 7, 12027 (2016). https://doi.org/10.1038/ncomms12027
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms12027
This article is cited by
-
Ultrafast electron dynamics in a topological surface state observed in two-dimensional momentum space
Scientific Reports (2023)
-
Visualizing discrete Fermi surfaces and possible nodal-line to Weyl state evolution in ZrSiTe
npj Quantum Materials (2022)
-
Designing light-element materials with large effective spin-orbit coupling
Nature Communications (2022)
-
Ambi-chiral anomalous Hall effect in magnetically doped topological insulators
Science China Physics, Mechanics & Astronomy (2022)
-
Probing topological quantum matter with scanning tunnelling microscopy
Nature Reviews Physics (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.