Abstract
Technological applications of novel metastable materials are frequently inhibited by abundant defects residing in these materials. Using first-principles methods, we investigate the defect thermodynamics and phase segregation in the technologically important metastable alloy GaAsBi. Our calculations predict defect energy levels in good agreement with those from numerous previous experiments and clarify the defect structures giving rise to these levels. We find that vacancies in some charge states become metastable or unstable with respect to antisite formation, and this instability is a general characteristic of zincblende semiconductors with small ionicity. The dominant point defects that degrade the electronic and optical performances are predicted to be AsGa, BiGa, AsGa+BiAs, BiGa+BiAs, VGa and VGa+BiAs, of which the first four and last two defects are minority-electron and minority-hole traps, respectively. VGa is also observed to have a critical role in controlling metastable Bi supersaturation by mediating Bi diffusion and clustering. To reduce the influences of these deleterious defects, we suggest shifting the growth away from an As-rich condition and/or using hydrogen passivation to reduce the minority-carrier traps. We expect this work to aid in the applications of GaAsBi for novel electronic and optoelectronic devices and to illuminate the control of deleterious defects in other metastable materials.
Similar content being viewed by others
Introduction
The metastable alloy GaAsBi has been intensely studied since its first successful fabrication by metalorganic vapor phase epitaxy in 19981 and by molecular beam epitaxy in 20032 owing to three key advantages over other GaAs-based compounds. First, Bi atoms reduce the band gap much more effectively than other alloying elements, such as In (≈83 meV per Bi% versus ≈15 meV per In%).3 Second, Bi incorporation dramatically decreases the temperature dependence of the electronic properties. For instance, a GaAsBi film with 2.6% Bi has a temperature coefficient of the band gap only 1/3 of that of GaAs near room temperature.4 This property can lead to the realization of temperature-insensitive devices,5 as confirmed in a study of GaAsBi-based laser diodes,6 and benefits a number of technologies. Third, Bi atoms strongly increase the spin-orbit splitting of GaAsBi, and for Bi contents near 10%, it is expected to totally suspend one type of Auger recombination,3, 5 which induces the serious ‘efficiency droop’ in high-energy light-emitting diodes and laser diodes. These advantages indicate that GaAsBi would provide a major improvement in many semiconductor devices as long as high-quality materials with a significant Bi content can be obtained.
However, Bi has a very low solubility in GaAs; the incorporation of a large Bi content (~10%) with low defects and without phase segregation is especially challenging.7 In the usual growth temperature range of GaAs, 500–600 °C, the Bi incorporation is nearly zero, which has been confirmed by both experiments8 and theoretical claculations.9 To enhance the Bi incorporation, growth temperatures as low as 300–400 °C are widely used to decelerate the growth dynamics that lead to low Bi incorporation. However, the low growth temperature also induces numerous defects, which result in short carrier lifetimes and low photoluminescence intensity.10, 11 Additionally, a previous theoretical study12 has shown that the dynamic processes associated with As substituting Bi, which limits Bi incorporation, are still extremely rapid at low temperatures, for example, <10−6 s at 320 °C. Thermal annealing has been used to reduce the defects, but the incorporated Bi atoms often segregate and form Bi-rich clusters.13 These defect-related issues have become a bottleneck in the successful applications of GaAsBi. For instance, to date, GaAsBi-based laser diodes require a threshold current density (2–10 kA cm−2)6, 14, 15, 16 that is approximately an order of magnitude higher than that of typical InGaAs-based laser diodes (0.2–0.5 kA cm−2).
Here we address the following essential questions related to the defects in GaAsBi: What are the primary intrinsic point defects, and how do they interact to form pair defects under equilibrium conditions? How do the defects affect the minority-carriers? Which defects mediate the formation of Bi-rich clusters during thermal annealing? Finally, how can one reduce the deleterious effects of the dominant defects? Our results are predominantly based on the thermodynamic properties of defects, which are expected to provide a useful guide to many aspects of defect behavior, even under non-equilibrium conditions. Additionally, we will qualitatively discuss non-equilibrium effects when the equilibrium results become invalid.
Materials and methods
In this paper, we examine six point defects: VGa, VAs, AsGa, GaAs, BiAs and BiGa. The interstitial defects of As and Ga are known for their high formation energies in GaAs17, 18 and are therefore excluded, as is the Bi interstitial. To determine how the dominant point defects interact with each other, we further examine thirteen pair defects, each consisting of two nearest-neighbor point defects. Motivated by the findings on pair defects, we examine eight clusters involving Bi defects with and without vacancies to explore the formation of Bi-rich clusters. Finally, we investigate eight defects involving H to examine the effects of hydrogen passivation.
We carry out ab initio calculations using density functional theory, as implemented in the Vienna ab initio Simulation Package.19 An energy cutoff of 400 eV is set to the plane-wave basis set, and the following projector-augmented wave potentials are utilized: Ga_GW(4s24p1) for Ga, As_GW(4s24p3) for As, Bi_d_GW(5d106s26p3) for Bi and H_GW(1s1) for H. These GW potentials generally give better properties for excited electronic states than the standard density functional theory potentials, and they are therefore appropriate for our defect calculations involving charge transfer to excited states. The HSE0620 hybrid functional is used to correctly describe the band gap. The predicted band gap of the bulk GaAs using HSE06 is 1.38 eV, which is consistent with the experimental value of 1.42 eV at 300 K.21 To describe the strong special relativity effects in the Bi atom, the spin-orbit coupling is included for the calculations involving Bi. The predicted spin-orbit splitting at the Γ point is 0.39 eV for bulk GaAs, which is in excellent agreement with the experimental value of 0.34 eV at 300 K.21 In Supplementary Figure S1, we demonstrate the importance of using both HSE06 and spin-orbit coupling by showing the notable differences in the defect formation energies using different methods. In our HSE06 calculations, the supercell size is 2 × 2 × 2, with a volume of 11.23 Å3, and the k-point sampling is a 4 × 4 × 4 Monkhorst-Pack grid. The ab initio method proposed by Freysoldt, Neugebauer and Van de Walle (FNV)22 is adopted to remove the image charge interaction and adjust the potential alignment between the perfect and defected structures. Our tests suggest that the error in the defect formation energy after the FNV correction is limited to approximately 0.1 eV (Supplementary Figure S2). Symmetry is broken to allow a possible Jahn–Teller distortion around the defects. To automatically generate the initial structures, manage the workflow and postprocess the results, the high-throughput computational tool, MAterials Simulation Toolkit23 is used. Note that the three major factors,24 namely, correct description of the band gap, proper removal of the image charge interaction and proper potential alignment, are critical to obtain reliable defect formation energies. Inadequate treatment of these three factors in previous studies of bulk GaAs resulted in scattered data (Supplementary Figure S3).
The defect formation energy Ef of a defect AB (atom A on host site B) with a charge state q is defined in Equation (1),24

where  and Etot(GaAs) are the total internal energies of the system with defect
and Etot(GaAs) are the total internal energies of the system with defect  and the perfect bulk GaAs, respectively; EFNV, EVBM and EF are the FNV correction, valence band maximum (VBM) energy and Fermi energy relative to the VBM energy, respectively; the chemical potentials μX for X=Bi, As and Ga at different conditions are summarized in Table 1. The lowest defect formation energy of a defect,
and the perfect bulk GaAs, respectively; EFNV, EVBM and EF are the FNV correction, valence band maximum (VBM) energy and Fermi energy relative to the VBM energy, respectively; the chemical potentials μX for X=Bi, As and Ga at different conditions are summarized in Table 1. The lowest defect formation energy of a defect,  , is determined by the minimum value of different charge states,
, is determined by the minimum value of different charge states,

Defect energy levels correspond to the EF where the slope of  changes and the levels are independent of the chemical potential. To explore the interaction between different defects, we define the binding energy, Eb, of a complex defect by Equation (3).
changes and the levels are independent of the chemical potential. To explore the interaction between different defects, we define the binding energy, Eb, of a complex defect by Equation (3).

where the complex defect AB+CD consists of defects AB and CD bound together.
Results and discussion
Metastability of defects involving vacancy
Our first finding is that in certain charge states, when the formation energies are typically very high, the point and pair defects involving vacancy become metastable or unstable. This instability means that the cation and anion vacancies can transform between each other with the assistance of an antisite defect, a phenomenon that was first theoretically discovered for isolated VAs and VGa over 30 years ago.26, 27 Table 2 shows that VAs can change to VGa+GaAs at the 2− and 3− charge states and that VGa can change to VAs+AsGa at the 1+, 2+ and 3+ charge states. As we will show later in Figure 1a, these charge states correspond to VAs and VGa with high formation energies relative to the other charge states. Because VAs and VGa at the aforementioned charge states are metastable, one needs to directly examine the ‘swapped’ structures to reveal their greater stability, which possibly explains the disregarding of these swapped structures in recent studies of GaAs.18, 28, 29 The anion (cation) vacancy in the pair defects VAs+BiAs, VGa+BiGa, VGa+AsGa and VGa+BiAs at certain charge states can all undergo similar structural changes to a more stable form, with a cation (anion) vacancy and an antisite replacing the original vacancy. The three other pair defects, VAs+BiGa, VAs+AsGa and VGa+GaAs, can change to a more stable form at certain charge states by hopping the Bi, As and Ga to the neighboring vacancy, respectively.
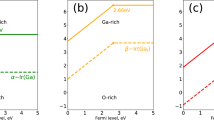
Lowest defect formation energy versus Fermi energy for (a) point defects and (b, c) pair defects under the As-rich condition. The dashed branches correspond to the stable swapped structures listed in Table 2; in (a), the metastable states of VGa and VAs are shown for reference. The results of the pair defects are plotted in two panels for easy visualization.
Experimental observation of the aforementioned metastability can be challenging because it occurs under conditions at which the defects have relatively high formation energies and therefore low concentrations, for example, an n-type doping condition for VAs and a p-type doping condition for VGa. Nevertheless, a possible experimental observation of the change VAs+AsGa→VGa was suggested in an early deep-level transient spectroscopic study,30 which claimed that the signal decrease of VAs+AsGa was accompanied by the signal increase of VGa during the treatment of n-type GaAs using ultrasonic vibration. To explore the generality of vacancy metastability in compound semiconductors, we examine the anion vacancy of 12 zincblende binary compounds, including ZnO, SiC and 10 III–V compounds. The results indicate that the metastability is closely related to ionicity: all the examined compounds with an ionicity of <0.5 undergo a similar change as VAs in GaAs (Supplementary Table S1).
Formation energy of point and pair defects
Figure 1a shows the defect formation energy of the point defects under the As-rich condition, which is widely employed by providing an excessive amount of As reactant in the growth chamber. The influence of other chemical potentials on the defect formation energy will be discussed at the end of this paper. The aforementioned metastability significantly changes the properties of VGa and VAs under the p- and n-type doping conditions, respectively. The dominant defects are AsGa2+, BiGa2+ and BiAs0 in the p-type films, whereas the dominant defects are VGa3− and BiAs0 in the n-type films. By contrast, VAs and GaAs have much larger formation energies and are expected to have insignificant concentrations at or near thermal equilibrium. Note that, although BiAs and BiGa do not have the lowest defect formation energy under most doping conditions, their non-equilibrium contents are expected to be dominant because of the significant (typically >1%) overall Bi content in most GaAsBi films.
Notably, under the condition EF<0.21 eV, the equilibrium content of BiGa2+ is predicted to be substantially more than that of BiAs0. This prediction suggests that the usual assumption that the incorporated Bi primarily substitutes As owing to their chemical similarity does not hold under certain growth conditions. A previous growth of Bi-doped GaAs using the liquid-encapsulated Czochralski method indeed found a significant amount (~10%) of Bi in the form of BiGa.31 It is worth noting that another study32 estimated the maximum ratio of BiGa as only ~5% of the total incorporated Bi atoms. That estimation was based on a fitting of the theoretical structural expansion around BiAs and BiGa with experimental X-ray absorption spectra, and a fundamental parameter utilized was that the Bi-As bonds around BiGa are 0.15 Å longer than the Bi-Ga bonds around BiAs. However, our calculations indicate that the aforementioned bond length difference varies dramatically with the charge state of BiGa. Namely, the Bi-As bonds around BiGa2+, BiGa+ and BiGa0 are 0.05, 0.11 and 0.15 Å longer than the Bi-Ga bonds around BiAs0, respectively. The previous study therefore applied bond lengths, which were appropriate for only the structures of BiGa0 and BiAs0. If BiGa2+ in the p-type films were considered, the fitting would yield a significantly higher fraction of BiGa. Because BiGa possesses deep energy levels, which are significant carrier traps as discussed below, but isolated BiAs does not, further experimental verification of the Bi substitution sites under different growth conditions is a critical requirement.
To verify our results, we compare the predicted energy levels of the point defects with available experimental data in Figure 2. We find that the average deviation between our predictions and the experimental values is 0.06 eV, which is encouraging given the much larger deviation found in previous theoretical studies (Supplementary Figure S3). For the most extensively studied defect AsGa, which corresponds to the EL2 peak in deep-level transient spectroscopic experiments, our predicted positions are 0.46 and 0.84 eV for the 2+/+ and +/0 energy levels, which agree reasonably well with the average experimental values of 0.49 and 0.72 eV, respectively.
Comparison between defect energy levels obtained from experiments and predictions by this work. The error bars represent the range of different values of the experimental data (VGa from refs 33, 34, VAs from refs 35, 36, AsGa from refs 31, 37, 38, 39 and GaAs from refs 40, 41, 42) or the supercell convergence errors of the theoretical data.
Additionally, our results question the accuracy of earlier reports on the energy levels of VAs and BiGa. As shown in Figure 2, the two energy levels of VAs near the conduction band minimum were identified as +/0 and 0/− by Saarinen et al.35 but 0/− and −/2− by Loualiche et al.33, both of which are different from our prediction of −/2− and 2−/3−. Kunzer at al.31 conjectured that the energy levels of BiGa2+/+ and BiGa+/0 lie in the ranges of 0.72–0.77 eV and 0.92–1.07 eV, respectively, which deviate significantly from our predictions of 0.33 and 0.80 eV, respectively.
Figures 1b and c show the defect formation energies of the pair defects. We find that the dominant pair defects originate from the combinations of dominant point defects (AsGa, BiAs, BiGa and VGa). Under p-type conditions, the dominant pair defect is (AsGa+BiAs)2+. Although (AsGa+AsGa)2+,3+ also has relatively low formation energies under p-type conditions, we will later show that two AsGa defects have a repulsive interaction under such conditions; thus the formation of the pair is unlikely. Under n-type conditions, the dominant pair defects are (VGa+BiAs)3− and (VGa+AsGa)1−, 2−, both of which involve VGa. It should be noted that the non-equilibrium growth of most GaAsBi films leads to much higher total Bi contents than the equilibrium values. To determine the potential influences of non-equilibrium conditions on Bi defects, we calculate the defect formation energies for a fixed total Bi content of 1%, which is established by allowing the Bi chemical potential μBi to vary with EF, as required (see Supplementary Information V). We find that five Bi defects: BiAs, BiGa, BiGa+BiAs, BiAs+BiAs and VGa+BiAs would have significant concentrations in certain regions of EF (Supplementary Figure S4).
From the determinations above, we can now clarify the nature of the majority-carrier traps reported by recent deep-level transient spectroscopic experiments on GaAsBi.43 As listed in Table 3, the three experimental majority-electron traps in n-type films can be assigned to our predicted primary defect levels of (VGa+BiAs)2−/3−, VGa2−/3− and (VGa+BiAs)−/2−, with an average deviation of ~0.12 eV between the experiments and this work. For the six majority-hole traps in p-type films, the three highest energy levels can be assigned to {BiGa+/0, AsGa+/0, (AsGa+BiAs)+/0, (BiGa+BiAs)+/0}, {AsGa2+/+, (AsGa+BiAs)2+/+, (BiGa+BiAs)2+/+} and BiGa2+/+, with an average deviation of ~0.04 eV between the experiments and this work. As we will show later, the lowest defect level at 0.08 eV could be assigned to Bi-rich clusters with vacancies, such as VAs+4BiAs and VGa+4BiAs. The nature of the energy levels at 0.12 and 0.17 eV is unclear, and they could be ascribed to unexplored complex defects and/or impurities in the films.
Influences of defect energy levels on minority-carriers
To identify the most deleterious defect energy levels to minority-carriers, which are critical to the electron–hole recombination in optoelectronic devices, we show the strength of minority-carrier trapping as a function of the Fermi energy for each defect energy level in Figure 3. The trapping rate44 of the minority-electron (minority-hole) for a given defect energy level, re-trap (rh-trap), is determined by the product of three factors, namely, the defect concentration, cd, the non-occupancy fraction of the defect energy level for the electron (hole), fe,l (fh,l) and the capture cross-section of the electron (hole), σe (σh):

Here  , n0 is the possible sites for the defect and El is the position of the defect energy level. Previous studies have found that the Coulomb interaction between the carriers and defects has a critical role: the typical capture cross-sections of repulsive centers, neutral centers and attractive centers are 10−8–10−5, 10−1–101 and 101–104 Å2, respectively.45 We approximate σe and σh as the intermediate values of the abovementioned ranges, as written in Equation (5).
, n0 is the possible sites for the defect and El is the position of the defect energy level. Previous studies have found that the Coulomb interaction between the carriers and defects has a critical role: the typical capture cross-sections of repulsive centers, neutral centers and attractive centers are 10−8–10−5, 10−1–101 and 101–104 Å2, respectively.45 We approximate σe and σh as the intermediate values of the abovementioned ranges, as written in Equation (5).

where q is the charge state of the defect. Tests show that the exponential prefactor dominates Equation (4), and even two orders of uncertainty of σe and σh results in minor changes to Figure 3.
Figure 3 shows that the minority-electron traps are dominated by AsGa, BiGa, AsGa+BiAs and BiGa+BiAs under p-type doping conditions and the minority-hole traps are dominated by VGa and VGa+BiAs under n-type doping conditions. Note that, because BiGa+BiAs is expected to have a significant concentration under non-equilibrium conditions (Supplementary Figure S4) despite its high defect formation energy, we reduce Efmin by 0.43 eV per Bi atom for all Bi defects (an amplitude corresponding to half of the μBi decrease at the VBM in the aforementioned non-equilibrium estimation) to include BiGa+BiAs in Figure 3. A similar figure without this correction can be found in Supplementary Figure S5. As all the primary traps contain at least one of the unwanted point defects, AsGa, BiGa and VGa, one should be able to effectively minimize the traps by an efficient reduction of the three point defects.
Binding energy of pair defects and formation of Bi-rich clusters
To determine how point defects interact and form pair defects (important processes during thermal annealing), we plot the binding energy of pair defects (Figure 4). We find that BiAs+BiAs has slightly negative (−0.02 eV) binding energies in the entire range of Fermi energy. BiGa+BiGa, AsGa+AsGa and AsGa+BiGa have positive binding energies when EF is less than 0.29, 0.40 and 0.65 eV, respectively, and slightly negative binding energies otherwise. In view of their relatively high formation energies (Figure 1c), the three pair defects are expected to form in a small quantity over a limited range of Fermi energy. By contrast, all the other pair defects, including those with high contents under equilibrium or non-equilibrium conditions (AsGa+BiAs, BiGa+BiAs and VGa+BiAs), possess negative binding energies in the entire range of Fermi energy. The pair defects involving Bi and vacancies have particularly low binding energies; thus the Bi–vacancy pairs likely provide the nuclei of the Bi-rich clusters during thermal annealing. Although BiGa+GaAs also has low binding energy, its overall formation energy is >3.1 eV (Figure 1c), which means that its content should be low, even in the presence of a significant Bi content under non-equilibrium conditions (Supplementary Figure S4).
To further examine whether a vacancy can bind multiple Bi defects together, we study relatively large clusters with and without a vacancy in the cluster center, namely, nBiAs, nBiGa, VGa+nBiAs and VAs+nBiAs (n=3 and 4). It turns out that pure Bi clusters have repulsive interactions in most regions of EF, but a vacancy strongly binds the Bi defects together (Supplementary Figure S6). Such behavior can be partially attributed to the compensation of the strain induced by Bi defects and vacancies. Our results support and extend the conclusion of a previous density functional theory study,46 which reported the nucleus effect of VGa0 in the formation of Bi-rich clusters using the LDA functional. In addition to the strong binding strength, the formation of Bi-rich clusters with vacancies rather than pure Bi clusters is supported by another fact: VAs+3BiAs, VAs+4BiAs and VGa+4BiAs possess energy levels 0.02–0.08 eV above the VBM (Supplementary Figures S6a and b), which agrees with previous experimental observations of Bi-included localized states 0.05–0.09 eV above the VBM.47 By contrast, all the examined pure Bi defects (mBiAs for m=1–4 and nBiGa for n=1–2) do not have similar energy levels.
In addition to serving as nuclei of the Bi-rich clusters, vacancies are expected to have a critical role in assisting the diffusion of Bi during the cluster formation, as the very large size of Bi atoms relative to Ga and As atoms makes it unlikely to be an interstitial diffuser. Unfortunately, the complete and quantitative modeling of the defect-mediated Bi diffusion over all possible Fermi levels and external chemical potentials is complex and beyond the scope of this paper. We therefore focus on building a simplified model under As-rich and n-type doping conditions. If we make a reasonable assumption that Bi diffuses by a vacancy-mediated mechanism with nearest-neighbor hops on either the Ga or As sublattice, then the diffusions must involve the formation of the pair defect VGa+BiGa or VAs+BiAs. Because VGa+BiGa is significantly more stable than VAs+BiAs for all Fermi levels (Figure 1b) and has a significantly stronger binding strength than VAs+BiAs for almost all Fermi levels (Figure 4), it is likely that the primary Bi diffusion path is through the VGa-mediated diffusion of BiGa. Additionally, Figure 1b shows that VGa+BiGa is stable in the 1− charge state over a wide range of Fermi energy. Therefore, we focus on BiGa diffusion through VGa-mediated hops, with the whole system in the 1− charge state; the diffusion of isolated VGa is assumed to be in the dominant 3− charge state.
We calculate the VGa-mediated BiGa diffusion using the well-known five-frequency model, as elaborated in Supplementary Information VIII. Six critical parameters for the model, namely, the migration barriers of processes 0–4 and the self-diffusivity of Ga, are found to be 2.16 eV, 2.47 eV, 1.79 eV, 2.54 eV, 1.98 eV and 4.3 × 1017 Å2 s−1, respectively. We observe that, in the typical annealing temperature range of 600–800 °C and annealing time range of 60–120 s, the diffusion length of BiGa is sufficiently long to promote the formation of Bi-rich clusters under the n-type doping condition. For example, a 60-s annealing at 800 °C leads to a BiGa diffusion length over 20 Å for EF>0.91 eV. By contrast, for a GaAsBi film with 1.0–3.0% uniformly distributed Bi atoms, the average distance between two neighboring Bi atoms is only approximately 16–11 Å. Therefore, VGa is capable of assisting BiGa diffusion to form Bi-rich clusters in typical GaAsBi films, with typical annealing temperatures and time. This mechanism of Bi clustering is also supported by the fact that VGa assists the diffusion of AsGa to form As-rich clusters during the thermal annealing of low temperature-grown GaAs.48, 49 Because of the strong binding between VGa and BiGa as well as the relatively fast VGa-mediated BiGa diffusion, we anticipate that the initial Bi-rich clusters consist of both Bi and VGa and that minimizing the content of VGa is expected to effectively reduce the formation of Bi-rich clusters under thermal annealing.
Å2 s−1, respectively. We observe that, in the typical annealing temperature range of 600–800 °C and annealing time range of 60–120 s, the diffusion length of BiGa is sufficiently long to promote the formation of Bi-rich clusters under the n-type doping condition. For example, a 60-s annealing at 800 °C leads to a BiGa diffusion length over 20 Å for EF>0.91 eV. By contrast, for a GaAsBi film with 1.0–3.0% uniformly distributed Bi atoms, the average distance between two neighboring Bi atoms is only approximately 16–11 Å. Therefore, VGa is capable of assisting BiGa diffusion to form Bi-rich clusters in typical GaAsBi films, with typical annealing temperatures and time. This mechanism of Bi clustering is also supported by the fact that VGa assists the diffusion of AsGa to form As-rich clusters during the thermal annealing of low temperature-grown GaAs.48, 49 Because of the strong binding between VGa and BiGa as well as the relatively fast VGa-mediated BiGa diffusion, we anticipate that the initial Bi-rich clusters consist of both Bi and VGa and that minimizing the content of VGa is expected to effectively reduce the formation of Bi-rich clusters under thermal annealing.
Hydrogen passivation of defects
To explore the methods of reducing the deleterious influence of defects, we first examine the hydrogen passivation of the dominant defects, a technology that is widely used in the silicon industry to reduce carrier traps. Figure 5a shows that hydrogen can effectively passivate VGa: the number of deep energy levels of VGa+nH is reduced from three to zero as the number of hydrogen atoms, n, increases from zero to three. Interestingly, adding a fourth hydrogen atom around VGa does not induce an extra defect energy level in the gap, which therefore allows a relatively wide range of hydrogen passivation conditions without the creation of new gap states. Thermodynamically, the H-passivated VGa are much more stable (over 0.53 eV per VGa) compared with the isolated VGa and hydrogen interstitial Hi, as shown in Figure 5c. Note that Hi is known to be able to exist in bulk GaAs under common metalorganic vapor-phase epitaxy conditions.50 Therefore, hydrogen passivation is likely to be realized, and it could effectively remove the defect levels induced by VGa. An additional advantage is that VGa is expected to diffuse significantly slower after passivation, which will reduce BiGa diffusion and, consequently, the formation of Bi-rich clusters. Because of the similarity between VGa and VGa+BiAs, it is likely that hydrogen passivation can also effectively remove the defect energy levels of VGa+BiAs.
Lowest defect formation energy of (a) VGa+nH and (b) BiGa+nH and binding energies of (c) VGa+nH and (d) BiGa+nH. (e) Lowest defect formation energy of Hi. The binding energy is relative to isolated Hi and VGa or BiGa. The chemical potential of H is selected as half of the energy of a H2 molecule (other choices of the chemical potential only shift the curve in (e) up or down). Several structures of VGa+nH, BiGa+nH and Hi can be found in Supplementary Figure S9.
In contrast to VGa, hydrogen passivation does not remove the deep defect levels of BiGa: both BiGa+H and BiGa+2H have two deep defect levels in the band gap, as is BiGa (Figure 5b). The binding energy of BiGa+H is positive at EF<0.29 eV (Figure 5d), indicating that H passivation cannot even be realized under such condition. For BiGa+2H, the two hydrogen atoms form a H2 molecule (Supplementary Figure S9) rather than bind to BiGa, and the shape of its defect formation energy curve resembles that of BiGa (Figure 5b).
Nevertheless, it is anticipated that hydrogenation would reduce the presence of defect BiGa by shifting up EF. Figure 1a shows that BiGa exists primarily under p-type conditions, and its formation energy increases with EF until 0.81 eV, where Hi is a donor (Figure 5e). Therefore, Hi will increase EF and exponentially decrease the equilibrium content of BiGa for EF<0.81 eV. Consistent with this prediction, previous experiments clearly showed that hydrogenation reduced the deep-level transient spectroscopic signal of AsGa in GaAs.51 Because of the similarity between BiGa and the three other primary defects, namely, AsGa, AsGa+BiAs and BiGa+BiAs, it is likely that hydrogenation would have similar effects on them.
However, because Hi introduces a defect level at 0.89 eV (Figure 5e), which would negatively impact device performance, it is necessary to gradually increase the hydrogenation to identify the conditions that lead to the best device performance. Consistent with this observation, previous experiments determined that moderate hydrogenation prominently increased the photoluminescence intensity of GaAs, but high hydrogen doses worsened it.52
Influence of external chemical potentials
Another method to potentially reduce the unwanted defects is by manipulating the external chemical potentials of Ga, As and Bi, which do not affect the positions of the defect energy levels but strongly influence the defect formation energies. Figures 6a–c show the formation energies of the point defects under As-rich, intermediate and Ga-rich conditions, respectively. The formation energies of defects involving the As site, namely, VAs, GaAs and BiAs, dramatically decrease when the chemical potential changes from more As-rich to more Ga-rich conditions, whereas the defects involving the Ga-site, namely VGa, AsGa and BiGa, sharply increase accordingly. Indeed, previous experiments found that the VGa content increases with the As vapor pressure.33 Among the three conditions, the intermediate and Ga-rich conditions generate the fewest unwanted defects for the n- and p-type films, respectively. By contrast, the usual As-rich condition generates a significant number of unwanted defects for both types of doping.
Lowest defect formation energy of point defects under the (a) As-rich, (b) intermediate and (c) Ga-rich conditions. The magenta and blue dashed branches correspond to the swapped structures of VGa and VAs, respectively, as presented in Table 2.
To avoid the As-rich growth condition, we suggest a more precise introduction of the As reactant, for example, using a pulsed As beam/precursor rather than filling the entire growth chamber with excessive As reactant, a method having also been proposed to increase the Bi ratio in GaAsBi.12 Additionally, one might explore the pulsed laser deposition method,53 which uses the plasma produced from bulk GaAs as the reactant and thus creates chemical potentials close to the intermediate condition.
Summary
In summary, we investigate the defect thermodynamics and Bi segregation in GaAsBi using density functional theory. We obtain defect energy levels that correspond reasonably well to the measured levels in GaAs and GaAsBi alloys and provide valuable insight into the nature of previously observed defect energy levels in GaAsBi. We find that a cation (anion) vacancy can change to an anion (cation) vacancy at certain charge states, and this phenomenon exists in a number of semiconductors with low ionicity. Under the usual As-rich growth condition, AsGa, BiGa, AsGa+BiAs and BiGa+BiAs are the major minority-electron traps in p-type films, whereas VGa and VGa+BiAs are the major minority-hole traps in n-type films. We predict that VGa serves as the nuclei of the Bi-rich clusters and assists the diffusion of Bi defects. To reduce the deleterious effects of defects, we propose using hydrogen passivation to decrease the minority-carrier traps and/or changing the growth to the Ga-rich or intermediate chemical potential conditions.
References
Oe, K. & Okamoto, H. New semiconductor alloy GaAs1-xBix grown by metal organic vapor phase epitaxy. Jpn J. Appl. Phys. 37, L1283 (1998).
Tixier, S., Adamcyk, M., Tiedje, T., Francoeur, S., Mascarenhas, A., Wei, P. & Schiettekatte, F. Molecular beam epitaxy growth of GaAs1-xBix . Appl. Phys. Lett. 82, 2245 (2003).
Li, H. & Wang, Z. M. Bismuth-Containing Compounds, (Springer: New York, USA, 2013).
Yoshida, J., Kita, T., Wada, O. & Oe, K. Temperature dependence of GaAs1-xBix band gap studied by photoreflectance spectroscopy. Jpn. J. Appl. Phys. 42, 371 (2003).
Broderick, C. A., Usman, M., Sweeney, S. J. & O'Reilly, E. P. Band engineering in dilute nitride and bismide semiconductor lasers. Semicond. Sci. Technol. 27, 094011 (2012).
Fuyuki, T., Yoshida, K., Yoshioka, R. & Yoshimoto, M. Electrically pumped room-temperature operation of GaAs1-xBix laser diodes with low-temperature dependence of oscillation wavelength. Appl. Phys. Express 7, 082101 (2014).
Beyer, A., Stolz, W. & Volz, K. Metastable cubic zinc-blende III/V semiconductors: growth and structural characteristics. Prog. Cryst. Growth Charact. Mater. 61, 46 (2015).
Richards, R. D., Bastiman, F., Hunter, C. J., Mendes, D. F., Mohmad, A. R., Roberts, J. S. & David, J. P. R. Molecular beam epitaxy growth of GaAsBi using As2 and As4 . J. Cryst. Growth 390, 120 (2014).
Jacobsen, H., Puchala, B., Kuech, T. F. & Morgan, D. Ab initio study of the strain dependent thermodynamics of Bi doping in GaAs. Phys. Rev. B 86, 085207 (2012).
Pacebutas, V., Bertulis, K., Aleksejenko, G. & Krotkus, A. Molecular-beam-epitaxy grown GaBiAs for terahertz optoelectronic applications. J. Mater. Sci. Mater. Electron. 20, 363 (2009).
Pačebutas, V., Butkutė, R., Čechavičius, B., Kavaliauskas, J. & Krotkus, A. Photoluminescence investigation of GaAs1−xBix/GaAs heterostructures. Thin Solid Films 520, 6415 (2012).
Luo, G. F., Yang, S. J., Li, J. C., Arjmand, M., Szlufarska, I., Brown, A. S., Kuech, T. F. & Morgan, D. First-principles studies on molecular beam epitaxy growth of GaAs1-xBix . Phys. Rev. B 92, 035415 (2015).
Wu, M. J., Luna, E., Puustinen, J., Guina, M. & Trampert, A. Formation and phase transformation of Bi-containing QD-like clusters in annealed GaAsBi. Nanotechnology 25, 205605 (2014).
Marko, I. P., Ludewig, P., Bushell, Z. L., Jin, S. R., Hild, K., Batool, Z., Reinhard, S., Nattermann, L., Stolz, W., Volz, K. & Sweeney, S. J. Physical properties and optimization of GaBiAs/(Al) GaAs based near-infrared laser diodes grown by MOVPE with up to 4.4% Bi. J. Phys. D Appl. Phys 47, 345103 (2014).
Marko, I. P., Jin, S. R., Hild, K., Batool, Z., Bushell, Z. L., Ludewig, P., Stolz, W., Volz, K., Butkute, R., Pacebutas, V., Geizutis, A., Krotkus, A. & Sweeney, S. J. Properties of hybrid MOVPE/MBE grown GaAsBi/GaAs based near-infrared emitting quantum well lasers. Semicond. Sci. Technol. 30, 094008 (2015).
Marko, I. P., Broderick, C. A., Jin, S. R., Ludewig, P., Stolz, W., Volz, K., Rorison, J. M., O'Reilly, E. P. & Sweeney, S. J. Optical gain in GaAsBi/GaAs quantum well diode lasers. Sci. Rep. 6, 28863 (2016).
Schick, J. T. & Morgan, C. G. Gallium interstitial contributions to diffusion in gallium arsenide. AIP Adv. 1, 032161 (2011).
Schick, J. T., Morgan, C. G. & Papoulias, P. First-principles study of As interstitials in GaAs: convergence, relaxation, and formation energy. Phys. Rev. B 66, 195302 (2002).
Kresse, G. & Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Heyd, J ., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 118, 8207 (2003).
Blakemore, J. S. Semiconducting and other major properties of gallium arsenide. J. Appl. Phys. 53, R123 (1982).
Freysoldt, C., Neugebauer, J. & Van de Walle, C. G. Fully ab initio finite-size corrections for charged-defect supercell calculations. Phys. Rev. Lett. 102, 016402 (2009).
Angsten, T., Mayeshiba, T., Wu, H. & Morgan, D. Elemental vacancy diffusion database from high-throughput first-principles calculations for fcc and hcp structures. New J. Phys. 16, 015018 (2014).
Freysoldt, C., Grabowski, B., Hickel, T., Neugebauer, J., Kresse, G., Janotti, A. & Van de Walle, C. G. First-principles calculations for point defects in solids. Rev. Mod. Phys. 86, 253 (2014).
Yamaguchi, K., Takeda, Y., Kameda, K. & Itagaki, K. Measurements of heat of formation of GaP, InP, GaAs, InAs, GaSb and InSb. Mater. Trans. JIM 35, 596 (1994).
Baraff, G. A. & Schluter, M. Bistability and metastability of the gallium vacancy in GaAs: the actuator of EL2. Phys. Rev. Lett. 55, 2340 (1985).
Baraff, G. A. & Schluter, M. Binding and formation energies of native defect pairs in GaAs. Phys. Rev. B 33, 7346 (1986).
El-Mellouhi, F. & Mousseau, N. Self-vacancies in gallium arsenide: an ab initio calculation. Phys. Rev. B 71, 125207 (2005).
Komsa, H.-P. & Pasquarello, A. Intrinsic defects in GaAs and InGaAs through hybrid functional calculations. Phys. B 407, 2833 (2012).
Wosinski, T., Makosa, A. & Witczak, Z. Transformation of native defects in bulk GaAs under ultrasonic vibration. Semicond. Sci. Technol. 9, 2047 (1994).
Kunzer, M., Jost, W., Kaufmann, U., Hobgood, H. M. & Thomas, R. N. Identification of the BiGa heteroantisite defect in GaAs:Bi. Phys. Rev. B 48, 4437 (1993).
Ciatto, G., Alippi, P., Bonapasta, A. A. & Tiedje, T. How much room for BiGa heteroantisites in GaAs1-xBix? Appl. Phys. Lett. 99, 141912 (2011).
Gebauer, J., Lausmann, M., Redmann, F., Krause-Rehberg, R., Leipner, H. S., Weber, E. R. & Ebert, P. Determination of the Gibbs free energy of formation of Ga vacancies in GaAs by positron annihilation. Phys. Rev. B 67, 235207 (2003).
Milnes, A. G. Impurity and defect levels (experimental) in gallium arsenide. Adv. Electron. Electron Phys 61, 63 (1983).
Saarinen, K., Hautojarvi, P., Lanki, P. & Corbel, C. Ionization levels of As vacancies in as-grown GaAs studied by positron-lifetime spectroscopy. Phys. Rev. B 44, 10585 (1991).
Loualiche, S., Nouailhat, A., Guillot, G. & Lannoo, M. Interpretation of deep-level optical spectroscopy and deep-level transient spectroscopy data: application to irradiation defects in GaAs. Phys. Rev. B 30, 5822 (1984).
Lagowski, J., Lin, D. G., Chen, T. P., Skowronski, M. & Gatos, H. C. Native hole trap in bulk GaAs and its association with the double-charge state of the arsenic antisite defect. Appl. Phys. Lett. 47, 929 (1985).
Weber, E. R., Ennen, H., Kaufmann, U., Windscheif, J., Schneider, J. & Wosinski, T. Identification of AsGa antisites in plastically deformed GaAs. J. Appl. Phys. 53, 6140 (1982).
Fuyuki, T., Kashiyama, S., Tominaga, Y., Oe, K. & Yoshimoto, M. Deep-hole traps in p-type GaAs1-xBix grown by molecular beam epitaxy. Jpn J. Appl. Phys. 50, 080203 (2011).
Wang, Z. G., Ledebo, L. A. & Grimmeiss, H. G. Electronic-properties of native deep-level defects in liquid-phase epitaxial GaAs. J. Phys. Condes. Matter 17, 259 (1984).
Elliott, K. R., Holmes, D. E., Chen, R. T. & Kirkpatrick, C. G. Infrared absorption of the 78-meV acceptor in GaAs. Appl. Phys. Lett. 40, 898 (1982).
Mihara, M., Mannoh, M., Shinozaki, K., Naritsuka, S. & Ishii, M. Photoluminescence of the 78 meV acceptor in GaAs layers grown by molecular beam epitaxy. Jpn. J. Appl. Phys. 25, L611 (1986).
Mooney, P. M., Tarun, M., Beaton, D. A., Mascarenhas, A. & Alberi, K. Deep level defects in dilute GaAsBi alloys grown under intense UV illumination. Semicond. Sci. Technol. 31, 085014 (2016).
Grove, A. S. Physics and Technology of Semiconductor Devices 130–131 (Wiley: New York, USA, 1967).
Stoneham, A. M. Theory of Defects in Solids: Electronic Structure of Defects in Insulators and Semiconductors, (Clarendon Press: Oxford, UK, 1975).
Punkkinen, M. P. J., Laukkanen, P., Kuzmin, M., Levamaki, H., Lang, J., Tuominen, M., Yasir, M., Dahl, J., Lu, S., Delczeg-Czirjak, E. K., Vitos, L. & Kokko, K. Does Bi form clusters in GaAs1-xBix alloys? Semicond. Sci. Technol. 29, 115007 (2014).
Yoshimoto, M., Itoh, M., Tominaga, Y. & Oe, K. Quantitative estimation of density of Bi-induced localized states in GaAs1-xBix grown by molecular beam epitaxy. J. Cryst. Growth 378, 73 (2013).
Bliss, D. E., Walukiewicz, W. & Haller, E. E. Annealing of AsGa-related defects in LT-GaAs: the role of gallium vacancies. J. Electron. Mater. 22, 1401 (1993).
Lochtefeld, A. J., Melloch, M. R., Chang, J. C. P. & Harmon, E. S. The role of point defects and arsenic precipitates in carrier trapping and recombination in low-temperature grown GaAs. Appl. Phys. Lett. 69, 1465 (1996).
Fushimi, H. & Wada, K. The presence of isolated hydrogen donors in heavily carbon-doped GaAs. J. Cryst. Growth 145, 420 (1994).
Lagowski, J., Kaminska, M., Parsey, J. M., Gatos, H. C. & Lichtensteiger, M. Passivation of the dominant deep level (EL2) in GaAs by hydrogen. Appl. Phys. Lett. 41, 1078 (1982).
Capizzi, M., Coluzza, C., Frankl, P., Frova, A., Colocci, M., Gurioli, M., Vinattieri, A. & Sacks, R. N. Picosecond spectroscopy of hydrogenated MBE-GaAs. Phys. B 170, 561 (1991).
Hung, W. K., Chern, M. Y. & Chen, Y. F. Epitaxial GaNxAs1-x layer formed by pulsed-laser irradiation of GaAs in an ambient nitrogen gas. Semicond. Sci. Technol. 15, 892 (2000).
Acknowledgements
This research was primarily supported by the NSF through the University of Wisconsin Materials Research Science and Engineering Center (Grant No DMR-1121288). Glen R Jenness and Zhewen Song were supported by the NSF Software Infrastructure for Sustained Innovation (SI2) award No 1148011. The authors gratefully acknowledge the use of computer clusters supported by the NSF through the University of Wisconsin Materials Research Science and Engineering Center (Grant No DMR-1121288). Computations in this work also benefited from the use of the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by the National Science Foundation Grant No ACI-1053575, the computing resources and assistance of the UW-Madison Center For High Throughput Computing (CHTC) in the Department of Computer Sciences and the National Energy Research Scientific Computing Center (NERSC), a DOE Office of Science User Facility supported by the Office of Science of the US Department of Energy under Contract No DE-AC02-05CH11231.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Supplementary Information accompanies the paper on the NPG Asia Materials website
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Luo, G., Yang, S., Jenness, G. et al. Understanding and reducing deleterious defects in the metastable alloy GaAsBi. NPG Asia Mater 9, e345 (2017). https://doi.org/10.1038/am.2016.201
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/am.2016.201
This article is cited by
-
Atomic-Resolution EDX, HAADF, and EELS Study of GaAs1-xBix Alloys
Nanoscale Research Letters (2020)
-
GaAs1-xBix growth on Ge: anti-phase domains, ordering, and exciton localization
Scientific Reports (2020)
-
Transition state redox during dynamical processes in semiconductors and insulators
NPG Asia Materials (2018)
-
Deep-level defects in n-type GaAsBi alloys grown by molecular beam epitaxy at low temperature and their influence on optical properties
Scientific Reports (2017)