Introduction

The strength of solids at temperature T=0 K limits the attainable range of elastic strain engineering,1 whereby finite elastic strain field2, 3 ɛ(x) is tuned to yield better transistors,1 solar cells,2 superconductors4 and other devices. Phonon instability5 controls the ideal strength6 and influences stress-driven defect nucleation and/or phase transformation in an initially perfect crystalline lattice at 0 K. When a phonon frequency ω becomes imaginary, the harmonic oscillation will grow in amplitude and subsequently break lattice translational symmetry leading to defect nucleation.7, 8

Such processes are believed to occur in some low-temperature nanoindentation experiments where near-ideal strengths are experimentally measured.6 Previous simulation studies have focused on the long-wave phonon instability (elastic instability) with wave vector k≈0 (Γ point) in the Brillouin zone (BZ) where an analytical formula can be derived based on the elastic constants and stress.7, 8, 9, 10, 11, 12 However, the long-wave instability is just one special class of the general phonon instability in full BZ,13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23 which may be diagnosed by phonon calculation for homogeneously strained crystals under periodical boundary conditions (PBCs).5 While for crystals with inhomogeneous strain during nanoindentation, where BZ and PBC become ill-defined as a result of losing the lattice translational symmetry, it is reasonable to turn to examine the structural stability of each infinite lattice Θ that is homogeneously strained according to the local deformation at each material point x, if the material strain field is slowly varied. This is because the incipient instability volume (centered at x) in nanoindentation with a smooth indenter is usually localized inside the material without the direct contact with the external indenter,7, 24, 25 and its size increases with a decreasing local strain gradient ∇E.26 When ∇E is rather small, the atomic configuration in would be significantly greater than the cutoff radius of the interatomic potential. It thus allows us, with diminishing error, to inspect the lattice stability of the infinite and homogeneously strained Θ instead of the inhomogeneous counterpart. To achieve this, development of new efficient algorithm is required, because in principle all the phonons in the full BZ (k space) of Θ for every material point within x space should be treated.

On the other hand, even if the soft phonons could be effectively pinpointed in crystals, it is still challenging to predict the final defect configuration. The unstable phonon mode indicates only the initial linear instability of atomic displacements, and as nonlinear effects develop, it becomes invalid as a descriptor at finite amplitude.15 In addition, a phonon is delocalized, and even a soft-phonon wave packet would span many atomic planes, whereas a defect such as a dislocation is localized down to one plane,26 implying that there should be a localization process during the evolution of a soft-phonon pack prior to defect nucleation. For a long-wave soft phonon, the localization process into a dislocation loop has been demonstrated.7, 8 Although the softening of finite-k phonons, particularly, the zone-boundary phonons, is quite common in shape-memory alloys,27 ferroelectric compounds28 and two-dimensional materials,18, 20, 23 their dynamical evolutions have not been previously reported.

In this paper, we develop a fast and robust full-BZ soft-phonon-searching algorithm called Phorion. Combining finite-element modeling incorporating Phorion and atomistic simulations, we show how a zone-boundary phonon instability is first triggered in a simple metal (aluminum) under nanoindentation and how it metamorphoses into a deformation twin (DT). We propose a general mechanism that governs the dynamical transformation of the soft short-wave phonons.

Materials and methods

Full-BZ soft-phonon-searching algorithm: Phorion

We design Phorion to capture soft phonons in the joint material-reciprocal (x–k) spaces, in which the positioning of the ‘softest’ phonon is treated as a linearly constrained optimization problem:

where x and k are constrained within the sample volume and the first BZ, respectively; ω is calculated by diagonalizing the k-dependent dynamical matrix and taking the lowest eigenvalue at each location x with the finite strain. The objective function f is set as rather than ω2 to prevent the minimum f (fmin) from being always pinned at the Γ point in the BZ during minimization. Obviously, once fmin is detected to first hit zero at (x*, k*) during the load ramp, the position x* and wave vector k*, as well as the polarization vector w* of the soft phonon can be determined. Because there exist multiple local minima for the linearly constrained optimization problem, we implement an effective strategy to capture the global minimum reliably and efficiently by taking and utilizing the analytical gradients of Equation (1) (see Supplementary Sec. I for details).

Finite-element modeling

We seamlessly incorporate Phorion into the interatomic potential finite-element model (IPFEM),7, 19 an extended local version of the quasicontinuum method.29 We then use the IPFEM-Phorion approach to simulate a cylindrical (111) indentation of a single crystal Al plate and pinpoint the phonon instability within the joint x–k space at 0 K. IPFEM simulation of nanoindentation is performed using the commercial finite-element software ABAQUS (Dassault Systèmes, Vélizy-Villacoublay, France) by writing the UMAT subroutine, with the Zope–Mishin embedded-atom method (EAM) potential of Al30 as the atomistic constitutive input. A single crystal Al plate, oriented as with a size of 2000 × 1000 Å in the x–y plane, is indented on its top surface of the (111) plane at 0 K by an analytical rigid cylindrical indenter with a radius of 500 Å lying along . The finite-element model, divided into 130 592 linear plane-strain elements, is free on the top surface, and is fixed at the bottom and in the x direction on both sides. The indentation proceeds in a displacement control with an indentation depth of 0.1 Å per step. Phorion is invoked at the end of each step.

Atomistic simulation

We use the LAMMPS code31 to perform the molecular dynamics (MD) simulation of nanoindentation. The size and boundary conditions of the indented Al plate in the x–y plane as well as the interatomic potential are the same as those in IPFEM simulation. PBC is applied in z, with half of the thickness greater than the cutoff radius given by the Zope–Mishin potential. About two million atoms are contained in the simulation box. Following ref. 24, nanoindentation is implemented by introducing an external repulsive potential acting upon the atoms on the top surface with a force constant of 10 eV Å−3; this virtual indenter proceeds at a speed of 1 m s−1. The time step is 1 fs, and the temperature is controlled at 1 K using an NVT ensemble with the Nosé–Hoover thermostat.32, 33

Ab initio calculation

To verify that the soft phonon predicted by IPFEM-Phorion based on the Zope–Mishin potential is real, we use the ABINIT code34 to perform an ab initio calculation of the phonon spectra of the homogeneously strained lattice at the predicted instability site. The Goedecker–Teter–Hutter Al pseudopotential is adopted within the local density approximation35, 36, 37 with a 20 Ha energy cutoff. Marzari’s ‘cold-smearing’ method38 is used for BZ integrations with a smearing parameter of 0.04 Ha. The lattice constant a0 of Al is first obtained using a 12 × 12 × 12 Monkhorst–Pack39 k-point grid and is found to be 3.99 Å, in good agreement with the experimental 4.03 Å40 value and the 4.05 Å value given by the Zope–Mishin potential. The Al lattice with the calculated a0 is then subjected to a homogeneous strain according to the local deformation gradient at the IPFEM-Phorion-predicted instability site; the phonon frequencies of which are calculated using the density functional perturbation theory41 with a 20 × 20 × 20 Monkhorst–Pack k-point grid.

Results and Discussion

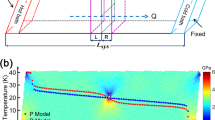
Figure 1a shows the indentation load (P) versus the indentation depth (h) response from the IPFEM simulation. With remarkable computational efficiency (Supplementary Sec. I), Phorion predicts that a zone-boundary phonon instability occurs inside the crystal at h=69.7 Å (Figure 1b), with a local Mises shear stress as large as 12.1 GPa. Examination of the phonon dispersion at the instability site based on the Zope–Mishin potential (Figure 1c) shows that a transverse acoustic phonon branch softens at L with a wave vector k* of and polarization vector . This soft mode is also verified by the ab initio calculation. To compare, we also utilize the acoustic tensor formalism42, 43 (equivalent to the Λ criterion7) within IPFEM to predict the onset of elastic (long-wave) instability. As shown in Figure 1a, the critical h is predicted to be 91.5 Å, occurring much later than the zone-boundary phonon instability. Moreover, the instability position and the mode are also different (Supplementary Figure S4).

Figure 1
figure 1

IPFEM-Phorion and MD simulations of (111) cylindrical nanoindentation of Al. The size of the Al plate in x–y plane is 2000 × 1000 Å and the indenter radius is 500 Å. (a) Load (P) versus indentation depth (h) by IPFEM and MD simulations. Phorion and the acoustic tensor formalism embedded in IPFEM predict a zone-boundary phonon instability and an elastic instability occurring at h=69.7 and 91.5 Å, respectively. (b) Contour of the objective function f in Equation (1) at h=69.7 Å by IPFEM-Phorion simulation, in which the wave vector k is fixed at . Homogeneous lattice instability site is indicated by the arrow, where f vanishes first at 184.6 Å beneath the top surface and 79.0 Å away from the central y axis. (c) Phonon spectra of the Al crystal lattice strained according to the local deformation gradient of the predicted lattice instability site shown in (b), based on the Zope–Mishin Al EAM potential (blue solid) and ab initio calculation using the Goedecker–Teter–Hutter Al pseudopotential (red dot). Both predict an acoustic phonon branch softening at . (d) Atomic configurations at the early stages of DT nucleation by MD simulation. Insets show magnified snapshots of how the DT is homogeneously nucleated. DT embryo center is positioned at 186.9 Å beneath the top surface and 80.7 Å displaced from the central y axis. Atoms are colored according to the central symmetric parameter.24 IPFEM, interatomic potential finite-element model; MD, molecular dynamics.

Full size image

To verify the bi-continuum prediction (joint x−k space), we have carried out direct MD simulation using the same empirical potential. As shown in Figure 1a, the P–h curves obtained by MD and IPFEM simulations agree very well before the first load drop in MD, and the critical h of 70.6 Å is very close to that predicted by Phorion, whereas the prediction by the k≈0 acoustic tensor criterion lags far behind. In MD, the load drop is found to correspond to the homogeneous nucleation of a DT, and the position of the DT embryo center agrees nearly perfectly with Phorion’s prediction (Figure 1d). The observed twinning plane of is consistent with k* provided by Phorion. However, the DT shear strain direction, which is , differs from the phonon polarization direction ; indeed, the two are perpendicular. This deviates greatly from the previous understanding for long-wave soft phonons.8 We also note a curious fact that the phonon-predicted (k*, w*) shear between adjacent atomic planes has zero Schmid factor in Figure 1b, so no mechanical work can be conducted during the initial bifurcation instability. It is then intriguing to connect the predicted soft-phonon mode with the homogeneous nucleation of the DT embryo.

To unravel this continuum-atomic connection, we perform a focused analysis of the evolution of Phorion-pinpointed soft phonon by direct MD simulation. First, an Al supercell under PBC is created with a homogeneous strain according to the local deformation gradient tensor at the instability site (Figure 1b), as shown in Figure 2a. It is oriented such that its x and z axes are along the soft phonon’s and plane normal, respectively. A low-amplitude (perturbational), high-wave vector atomic displacement wave according to the soft phonon’s polarization is then injected into the supercell (Figure 2a). Its ultrafast evolution dynamics are then traced directly with MD. Figure 2b shows the evolution of the perturbational wave prior to defect nucleation. It can be observed that, instead of continuous growth, the wave experiences an amplitude oscillation while keeping its original shape up to ~19.8 ps (Figure 2b I–IV). Then its upper and lower envelopes bend into sinusoidal shapes, and their amplitudes continue to grow until ~23.5 ps (Figure 2b V–VI). Finally, the envelope curves evolve into a defect embryo residing in only a couple of atomic layers and forms a conspicuous displacement shuffling along within the packet (Figure 2b VII–VIII).

Figure 2
figure 2

Structural metamorphosis of a perturbed Al supercell. (a) Al supercell under PBCs is subjected to the same strain as that at the lattice instability site predicted by Phorion shown in Figure 1b. It is perturbed by a plane wave according to the instability mode of the soft L phonon shown in Figure 1c, with an initial amplitude w0 of 0.01 Å. (b, d and e) Spatial evolutions of the displacements of the 36 atomic layers along x, y and z, respectively. (c) Temporal evolution of the displacements x of the atomic layers (in blue), which are initially bunched together in two groups, A1 and A2. They are compared with the linear exponential growth curves (in red), in which the L phonon’s imaginary circular frequency ω=0.406i THz. (f) Atomic configuration of the supercell at 24.05 ps, in which a deformation twin is nucleated. Atoms are colored according to the central symmetry parameter, with red atoms constituting two twinning planes. PBC, periodical boundary condition.

Full size image

To understand the zone-boundary phonon driven process above, we analyze the temporal evolution of the displacement in x (ux) of each atomic layer. As shown in Figure 2c, we may divide the odd- and even-numbered atomic layers into A1 and A2 groups, in which their ux are initially bunched together, thereby being grouped into the initial lower- and upper-straight envelope lines. Such bunching is maintained until ~19.8 ps, accounting for the undistortion of the wave profile shown in Figure 2b I–IV. During this stage, ux of A1 and A2 groups first follow linear exponential growth as with an imaginary ω within the harmonic approximation, where w0 is the initial amplitude of the perturbational wave. However, they then deviate from this pure amplitude growth and start to oscillate. Such a response is attributed to the anharmonic terms in the total potential energy expansion , where uA is the phonon displacement. The lack of the cubic term is owing to the symmetry of the zone-boundary phonon mode (see Supplementary Sec. III for the analytical expressions of ΔΨ). Figure 3 compares ΔΨ−uA of the harmonic expansion with that including the fourth-order anharmonic term. In contrast to a downward parabola of the harmonic expansion, the significant anharmonic effect yields a double-well potential, which in principle could arrest the perturbational wave and suppress the amplitude growth. The behavior of the injected wave in stages I–IV in Figure 2b could thus be understood. Indeed, using the Landau polynomials language of phase transitions, what Figure 3 describes is a phase transformation that should occur after the L-phonon ‘spinodal’ instability (in displacement, instead of chemical concentration) to a new crystal structure. In Figure 3, adjacent atomic layers undergo displacement shuffling along on the path from the center to one of the double wells, which is actually accompanied by a phase transformation from the original face-centered cubic (FCC) phase to a new triclinic (TRI) phase. As shown in the primitive cell of the TRI structure, there exist two basis atoms occupying two sites (denoted as B1 and B2) on adjacent atomic layers that exactly belong to the A1 and A2 groups, respectively.

Figure 3
figure 3

Response of the potential energy change (ΔΨ) of the Al supercell to the phonon displacement (uA) of the perturbational wave. ΔΨ can be fitted as (in blue), where c2=−0.993 eV Å−2 and c4=−949.7 eV Å−4, compared with the harmonic-approximation response following (in red), where N is the number of atoms in the supercell and m is the atomic mass of Al. Primitive cells of the FCC and TRI structures, corresponding to the center and the bottom of the double wells, respectively, are shown on the right, and they have . Two basis atoms in the TRI primitive cell are colored with gray and green, respectively. TRI, triclinic.

Full size image

However, this phase transformation, triggered by the zone-boundary soft phonon, does not significantly relax the strain energy, and the TRI phase is still subjected to high stress. Therefore, it is still necessary to keep inspecting its structural instability. If the TRI structure were mechanically stable, the injected perturbational and subsequently grown wave could be dissipated by phonon scattering44 and permanently arrested by the double-well potential, which would lead to a polymorphic phase transition such as those observed in some indentation experiments.45, 46 Otherwise, the second-generation lattice instability within the TRI structure would affect the wave growth and may drive it to escape from the TRI phase in a different direction not reflected in the Landau polynomial plot of Figure 3.

In fact, second-generation phonon spectra analysis shows that the TRI structure is elastically unstable for a long wave with (Figure 4a), where [001]TRI is a reciprocal vector to the real-space lattice vectors of TRI shown in Figure 3. For the present supercell with a limited size along z, only a soft phonon with k of is allowed to be excited and is expected to generate two independent unstable long waves denoted as β1 and β2 that involve the collective movement of the B1- and B2-sited (or A1- and A2-grouped) atoms, respectively. Eigenmode analysis shows that each of the long waves can be decomposed into three polarization components including two transverse waves and oscillating along x and y, respectively, and a longitudinal wave oscillating along z (i=1, 2), with their normalized amplitudes v and phase ϕ shown in Supplementary Table S3. As the displacement shuffling along breaks the central symmetry of B1- and B2-sited atoms in the TRI structure, these polarization components have different phases, yielding a double-helix profile for the β1–β2 pair (Figure 4b). For the and waves, owing to a phase difference of π, their superposition upon the original injected wave would bend its lower and upper envelope lines into a pair of sinusoidal curves oscillating oppositely and coherently, and drive the system to escape from the double-well potential; this explains the profile of the injected wave shown in Figure 2b V. The continuous amplitude growth of the sinusoidal envelope curves (Figure 2b VI) followed by progressive localization (Figure 2b VII–VIII) agrees well with the localization behavior of an unstable elastic wave,8 even though ‘wave-front steepening’ that breaks the positive strain–negative strain symmetry is not observed, resulting from the vanishing shear stress component τzx=0 (zero Schmid factor) here.

Figure 4
figure 4

Near-Γ phonon instability of the TRI structure. (a) Phonon spectra of the TRI structure along the Γ-Z path in the BZ. For the present supercell with , there are nine k points allowable distributed uniformly between (Γ, Z], of which the frequencies on the softened phonon branch are denoted as solid dots. Among these, only the k point at has an imaginary frequency, denoted as the red dot. (b) Wave profiles with normalized amplitudes of two unstable long waves β1 and β2 excited by the soft phonon denoted in (a). Two long waves spatially constitute a double helix, with their polarization components shown on the projective planes. BZ, Brillouin zone; TRI, triclinic.

Full size image

As indicated above, the TRI structure would also generate polarization components oscillating along y and z, which contribute to the DT nucleation as well. For the and waves with the same v and ϕ (Supplementary Table S3), they are expected to be merged into a single long wave βy with phase π/2 ahead of , involving collective displacements along y of all the A1- and A2-grouped atoms. Such a prediction is verified by tracing the evolution of uy for all the atomic layers, shown in Figure 2d. It can be observed that a single long uy wave is excited, followed by the amplitude growth (Figure 2d I–II), wave-front steepening (Figure 2d III), and shrinking into a couple of atomic layers and thus producing a uniform shear along (Figure 2d IV); this wave actually behaves as an unstable elastic wave.8 Simultaneously, a single uz wave also develops owing to crystallographic shear-tension coupling8 and experiences the dynamics similar to those of the uy wave (Figure 2e), albeit with much smaller amplitude.

Therefore, eventually, the TRI phase turns out to be just an intermediate product, decomposing within tens of picoseconds by the second-stage, near-Γ phonon instability to evolve into a lattice defect–DT, as shown in Figure 2f. Its atomic structure is verified to be consistent with that in Figure 1d, proving the continuum-atomic linkage and the validity of our bi-continuum prediction (joint x−k space) as well as focal study of nucleation dynamics with PBCs. Unexpectedly, and quite distinct from a conventional DT in which all atomic planes slip along the same direction (same Shockley partial Burgers vector) thereby producing a uniform shear strain, the DTs in Figure 1d and 2f have two different slip vectors alternating along and on every successive planes. In fact, our DT embryo is mainly achieved by the superposition of the displacement shuffling along resulting from the localization of the and waves, and the shear strain along contributed by the accumulated deformation before the L-phonon softening plus the localization of the βy wave (βz contribution can be neglected owing to a small amplitude). The two slip vectors are produced through and for adjacent planes, and the stacking order is thus changed from the original ‘’, for example, to ‘’. In other words, a DT with a width of nucleates homogeneously in the lattice (see Supplementary Figure S5 for the schematic of how the stacking order is changed). If viewed from , the DT has an averaged transformation shear along , where the average relative slip vector between two adjacent planes is , only 50% of that of the conventional textbook DT (Supplementary Figure S6), leading to a significantly smaller transformation strain and smaller elastic energy of embedding. Interestingly, our DT embryo shows a crude resemblance to the DT growing from a grain boundary following a dislocation-reaction and cross-slip mechanism recently proposed by Zhu et al.,47, 48 which also incorporates two different slip vectors or alternating Shockley partial Burgers vectors. To be revealed as the product of two degenerate soft phonons is quite a surprise, though.

Conclusions

In summary, we have developed a robust full-BZ soft-phonon-searching algorithm, which can be combined with other multiscale simulation methods or ab initio calculation tools to predict the lattice instability and the ideal strength of materials that enable elastic strain engineering.1 We have revealed how a continuum soft phonon evolves into a discrete atomic defect within tens of picoseconds in an indented perfect crystal at stress extreme. This involves four stages: (1) linear growth of an unstable short wave triggered by a softened L phonon, well described by the harmonic-approximation phonon theory; (2) arrest of the short wave by a double-well potential in the form of an anharmonic Landau polynomial, indicating a polymorphic phase transformation from FCC to TRI; (3) excitation of two independent unstable long waves by a soft near-Γ phonon in the TRI lattice; and (4) growth and localization of the two long waves until trapped in a couple of atomic layers, where an unconventional DT embryo with staggered slip Burgers vectors and 50% of the total transformation strain of the textbook FCC DT is formed. In this two-stage soft-phonon cascade, the Landau polynomial has a critical role, with the anharmonic energy terms arresting the dynamics of an L phonon in FCC followed by a near-Γ phonon in TRI. In Supplementary Sec. IV, we show an analytical scaling theory that explains why an unstable long elastic wave is much more difficult to be trapped in a polynomial energy landscape.

The Figure 3 scenario is not unlike the well-known temperature-driven phase transformation within a double-well potential49 in phonon coordinate. However, a salient feature of the stress-driven martensitic transformation owing to a softened zone-boundary phonon is that the new phase still withstands high stress, and it is thus highly likely to be unstable as well and prone to the next-stage evolution. This is because a first-generation transition yields little transformation strain, as the zone-boundary phonon has too short wavelength, unlike a long-wavelength phonon that can significantly relax the strain in a local region. In view of this, we believe that the proposed two-stage transformation mechanism can generally describe the dynamics of the homogeneous defect nucleation induced by a softened zone-boundary (or nearby) phonon at stress extremes. As we show in Supplementary Sec. V, it can also fully account for the homogeneous nucleation of a dislocation. The general utility of IPFEM-Phorion bi-continuum stability analysis has been repeatedly verified by our direct atomistic simulations. The uncovered material dynamics at stress extremes reveal deep connections between delocalized phonons in x and k continua—a wave phenomenon controlled by the harmonic part of potential—and localized atomic defects trapped by the full nonlinear interatomic potential energy landscape, which adds to the rich repertoire of nonlinear dynamics found in nature.50, 51